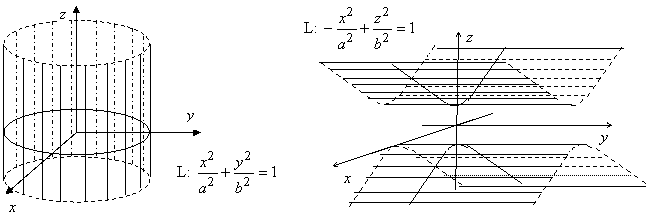 Аналогично изложенному доказывается, что цилиндрическая
поверхность с образующими, параллельными оси Oу,
определяется уравнением F(x,
z) = 0; поверхность с образующими, параллельными
оси Oх, определяется уравнением F(у, z) = 0.
Аналогично изложенному доказывается, что цилиндрическая
поверхность с образующими, параллельными оси Oу,
определяется уравнением F(x,
z) = 0; поверхность с образующими, параллельными
оси Oх, определяется уравнением F(у, z) = 0.
2.1.8.2.1. Эллиптический цилиндр.
Уравнение этой поверхности в случае, когда образующие параллельны оси Oz 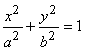 .
.
2.1.8.2.2. Гиперболический цилиндр.
Уравнение этой поверхности в случае, когда образующие параллельны оси Oу, а для направляющей действительной осью является Оу:
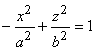 .
.
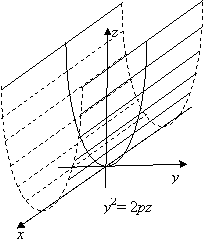 2.1.8.2.2. Параболический цилиндр.
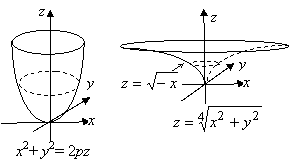
Уравнение y2= 2рz определяет параболический цилиндр с направляющей –
параболой, лежащей в плоскости Oyz и образующей, параллельной оси Oх.
2.1.8.2.2. Параболический цилиндр.
Уравнение y2= 2рz определяет параболический цилиндр с направляющей –
параболой, лежащей в плоскости Oyz и образующей, параллельной оси Oх.
 2.1.8.3. Поверхности вращения.
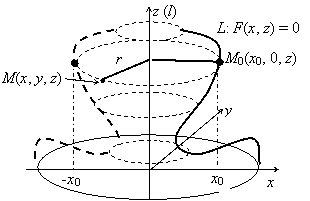
Пусть в плоскости задана прямая l и кривая L. Рассмотрим поверхность, которая образуется в результате
вращения L вокруг l
(каждая точка M0 кривой L движется по окружности, плоскость которой перпендикулярна
l и радиус которой равен расстоянию от M0 до l). Систему
координат выберем так, чтобы прямая l совпадала с осью Oz, а
плоскость, в которой лежат l и
L, была координатной плоскостью Oxz. Тогда кривая L
определяется некоторым уравнением F(x, z) = 0. Радиус r окружности, по которой движется
точка M0(x0,
0, z), равен расстоянию от этой точки до оси Oz, т.е.
2.1.8.3. Поверхности вращения.
Пусть в плоскости задана прямая l и кривая L. Рассмотрим поверхность, которая образуется в результате
вращения L вокруг l
(каждая точка M0 кривой L движется по окружности, плоскость которой перпендикулярна
l и радиус которой равен расстоянию от M0 до l). Систему
координат выберем так, чтобы прямая l совпадала с осью Oz, а
плоскость, в которой лежат l и
L, была координатной плоскостью Oxz. Тогда кривая L
определяется некоторым уравнением F(x, z) = 0. Радиус r окружности, по которой движется
точка M0(x0,
0, z), равен расстоянию от этой точки до оси Oz, т.е. ![]() . Если точка х0
удовлетворяет уравнению F(x0,
z) = 0, то любая точка окружности удовлетворяет
уравнению F(
. Если точка х0
удовлетворяет уравнению F(x0,
z) = 0, то любая точка окружности удовлетворяет
уравнению F(![]() , z) = 0, где знак выбирается в соответствии с sign x.
Таким образом, уравнение поверхности вращения будет
, z) = 0, где знак выбирается в соответствии с sign x.
Таким образом, уравнение поверхности вращения будет ![]() ,
где знак «+» берется, если поверхность порождается точками с положительной
абсциссой; если поверхность порождается точками с отрицательной абсциссой,
берется знак «-». Так, если мы вращаем вокруг оси Oz правую ветвь параболы
,
где знак «+» берется, если поверхность порождается точками с положительной
абсциссой; если поверхность порождается точками с отрицательной абсциссой,
берется знак «-». Так, если мы вращаем вокруг оси Oz правую ветвь параболы
х2 = 2рz,
уравнение поверхности вращения будет ![]() , или х2
+ у2= 2рz; такое
же уравнение получится, если вокруг оси Oz
вращается левая ветвь этой параболы:
, или х2
+ у2= 2рz; такое
же уравнение получится, если вокруг оси Oz
вращается левая ветвь этой параболы: ![]() ; эта поверхность
называется параболоидом вращения. Если же поверхность получена в результате
вращения вокруг оси Oz кривой
; эта поверхность
называется параболоидом вращения. Если же поверхность получена в результате
вращения вокруг оси Oz кривой ![]() , определенной при
, определенной при ![]() , то в ее уравнении мы должны
заменить х на
, то в ее уравнении мы должны
заменить х на ![]() , в результате получим
, в результате получим ![]() , или
, или ![]() ,
естественно, это поверхность уже не будет поверхностью второго порядка.
,
естественно, это поверхность уже не будет поверхностью второго порядка.
2.1.8.4. Канонические уравнения и изображения поверхностей второго порядка. При изучении нижеследующих поверхностей второго порядка мы будем пользоваться приемом, который называется методом сечений. Он заключается в том, что для изображения поверхности мы рисуем кривые, которые получаются при пересечении поверхности с координатными плоскостями и, при необходимости, с плоскостями, параллельными координатным и соображаем, как идет поверхность между этими сечениями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.