Федеральное государственное образовательное учреждение
высшего профессионального образования
«Сибирский Федеральный Университет»
ИНСТИТУТ ЦВЕТНЫХ МЕТАЛЛОВ И МАТЕРИАЛОВЕДЕНИЯ
Кафедра: Автоматизации производственных процессов
Специальность: 220301
Группа: АМЦ 05-2 (МФ 05-9)
Лабораторная работа №4
«Решение задач статической оптимизации в пакете математического моделирования MATLAB»
(2 вариант)
Преподаватель: Даныкина Г.Б.
Разработал студент: Ефимов М.Л.
Красноярск, 2009 г.
Цель работы: ознакомиться с основными командами программного пакета Optimization Toolbox системы MATLAB в оптимизационных задачах; научиться решать задачи статической оптимизации в системе MATLAB.
1. Оптимизация методом линейного программирования
Исходные данные:
Критерий: ![]() необходимо максимизировать;
необходимо максимизировать;
Ограничения:
![]()
![]()
![]()
![]()
Решение в ПП MATLAB имеет следующий вид:
>> f=[2; -3];
>> A=[1 2; -3 -2; 2 -1; 0 -1; -1 0];
>> b=[12; -8; 8; 0; 0];
>> [x,fval,exitflag,output]=linprog(f,A,b)
Optimization terminated successfully.
x =
0.0000
6.0000
fval =
-18.0000
exitflag =
1
output =
iterations: 5
cgiterations: 0
algorithm: 'lipsol'
2. Одномерная безусловная оптимизация
Исходные данные:
Критерий:
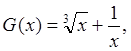
необходимо минимизировать.
Решение в ПП MATLAB имеет следующий вид:
>> f=inline('x^1/3+1/x');
>> x=fminsearch(f,1)
x =
1.7320
>> G =x^1/3+1/x
G =
1.1547
3. Многомерная безусловная оптимизация
Исходные данные:
Критерий:
![]()
необходимо минимизировать.
Начальные условия:
![]()
![]()
![]()
Решение в ПП MATLAB имеет следующий вид:
Способ №1:
Создаем m – файл:
function[f,g]=myfun(x)
f=(x(1)-2)^2+(3*x(2)-x(1))^2;
if nargout>1 %Проверка количества аргументов функции
g(1)=4*x(1)-4-6*x(2);
g(2)=18*x(2)-6*x(1);
end;
Далее в командной строке набираем:
>> options=optimset('GradObj','on');
>> x0=[1,1];
>> [x,fval]=fminunc('myfun',x0,options)
Optimization terminated successfully:
First-order optimality less than OPTIONS.TolFun, and no negative/zero curvature detected
x =
2.0000 0.6667
fval =
9.8608e-032
>> % Построение графика
>> [x,y]=meshgrid(-10: 0.1: 10);
>> f=(x-2)^2+(3*y-x)^2;
>> meshc(x,y,f)
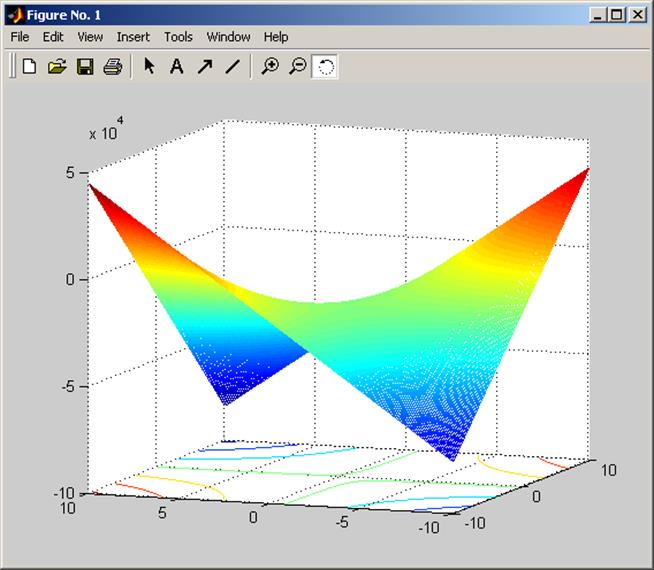
Рисунок 1 – Поверхность целевой функции
Способ №2:
Создаем m – файл:
function f=myfun2(x)
f=(x(1)-2)^2+(3*x(2)-x(1))^2;
Далее в командной строке набираем:
>> x0=[1,1];
>> [x,fval]=fminunc('myfun2',x0)
Warning: Gradient must be provided for trust-region method;
using line-search method instead.
> In D:\toolbox\optim\fminunc.m at line 211
Optimization terminated successfully:
Search direction less than 2*options.TolX
x =
2.0000 0.6667
fval =
4.7775e-016
Вывод: Решение математических задач, в частности задачи оптимизации, очень удобно производить в ПП MATLAB. Однако для этого требуется знание специфики задания условий задачи вычислительной машине, порядка ввода информации, а также знание синтаксиса языка MATLAB.
Результаты оптимизации полученные с помощью ПП MATLAB совпадают с результатами, полученными в ранее выполненных лабораторных работах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.