Градиентные методы. Метод градиентного спуска с постоянным шагом. Метод наискорейшего градиентного спуска. Метод покоординатного спуска

Если выбранное условие при текущем t_k не выполняется, шаг уменьшается вдвое и точка 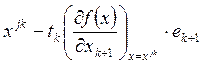 вычисляется заново. При фиксированном j за одну итерацию с номером k изменяется только одна проекция точки x^jk, имеющая номер k+ 1, а в течение всего цикла с номером j, т.е. начиная с    k = 0 и кончая k = n – 1, изменяются все n проекций точки x^j0. После этого точке x^jn присваивается номер x^j+1,0 и она берется за начальную точку для вычисления в j + 1 цикле. Расчет заканчивается в точке x^jk при выполнении по крайней мере одного из трех критериев окончания счета:  или j ≥ M, или двукратного выполнения неравенств , . Вопрос о том, является ли точка x^jk найденным приближением искомой точки, решается путем проведения дополнительного исследования.

Алгоритм

Шаг 1. Задаем x⁰⁰, e>0, e₁>0, e₂>0, предельное число M циклов счета, кратное n, где n – размерность вектора x. Находим градиент Ñf(x).

Шаг 2. Задаем номер цикла j = 0.

Шаг 3. Проверяем условие j ≥ M:

а) если j ≥ M, то x^*=x^jk, расчет окончен; б) если нет, то переходим к шагу 4.

Шаг 4. Задаем k=0.

Шаг 5. Проверяем условие k ≤ n – 1;

а) если k ≤ n – 1, то переходим к шагу 6;

б) если k = n, то полагаем j = j + 1 и x^j+1,k = x^jn и переходим к шагу 3.

Шаг 6. Вычисляем Ñf(x^jk).

Шаг 7. Проверяем выполнение критерия окончания :

а) если критерий выполнен, x^*=x^jk, расчет окончен;

б) если нет, то переходим к шагу 8.

Шаг 8. Задаем t_k.

Шаг 9. Вычисляем точку x^jk+1: .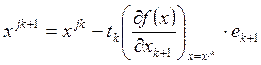

Шаг 10. Проверяем выполнение условия

 .

а) если условие выполнено, то переходим к шагу 11;

б) если нет, то полагаем 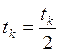 и переходим к шагу 9.

Шаг 11. Проверяем выполнение условий

 

а) если в двух последовательных циклах с номерами j и j – 1 оба условия выполняются, то расчет в точке x^jk+1 окончен и x^*=x^jk+1;

б) если хотя бы одно из условий не выполнено, полагаем k=k+1 и переходим к шагу 5.

Геометрическая интерпретация метода для n=2 приведена на рисунке 3.

Замечания: 1. Если функция f(x) удовлетворяет условиям утверждения 1, то построение последовательности {xk} по методу координатного спуска обеспечивает выполнение условия ||Ñf(xk)|| ® 0 при k®¥. 2. Найденная в результате применения метода точка xk нуждается в дополнительном исследовании с целью ее классификации. 3. Скорость сходимости метода оценивается как линейная (т.е. со скоростью геометрической прогрессии)

Рисунок 3

Метод Гаусса-Зейделя

Стратегия поиска

Стратегия метода Гаусса-Зейделя [Gauss-Seidel] состоит в построении последовательности точек {x^k}, k= 0, 1, …, таких, что f(x^k+1)<f(x^k), k= 0, 1, …. Точки последовательности {x^k} вычисляются по правилу

(6)

где j – номер цикла вычислений, j= 0, 1, 2, …; k – номер интеграции внутри цикла, k= 0, 1, …, n–1; e_k+1 – единичный вектор, (k+1)-я проекция которого равна 1; точка x⁰⁰ задается пользователем, величина шага t_k выбирается из условия

.

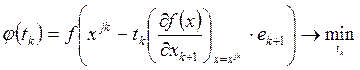Эта задача является задачей одномерной минимизации функции 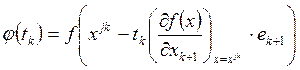 и может быть решена либо с использованием условий 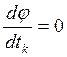, , 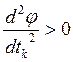либо численно с использованием методов одномерной минимизации, как задача .

Если условие 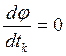 имеет высокую степень и корни его трудно определить, можно аппроксимировать функцию j(t_k) полиномом P(t_k) второй или третьей степени и определить t_k^* из условия , .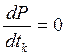

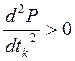При численном решении задачи определения величины шага степень близости найденного значения t_k к оптимальному значению t_k^*, удовлетворяющему условиям 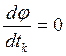, , 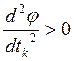зависят от задания интервала [a,b] и точности методов одномерной минимизации.

При фиксированном j за одну итерацию с номером k изменяется только одна проекция точки x^jk, имеющая номер k + 1, а в течение всего цикла с номером j, т.е. начиная с k = 0 и кончая k = n – 1, изменяются все n проекции точки x^j0. После этого точке x^jk присваивается номер x^j+1,0 и она берется за начальную точку для вычисления в (j + 1)-м цикле.

Расчет заканчивается в точке x^jk при выполнении по крайней мере одного из трех критериев окончания счета: , или k ≥ M, или двукратного выполнения неравенств , . Здесь e₁, e₁ – малые положительные числа, M – предельное число циклов итерации. Вопрос о том, является ли точка x^jk найденным приближением искомой точки, решается путем проведения дополнительного исследования.

Алгоритм

Шаг 1. Задаем x⁰⁰, e₁>0, e₂>0, предельное число M циклов счета, кратное n, где n – размерность вектора x. Находим градиент Ñf(x).

Шаг 2. Задаем номер цикла j = 0.

Шаг 3. Проверяем условие j ≥ M:

а) если j ≥ M, то расчет окончен и x^*=x^jk;

б) если j < M, то переходим к шагу 4.

Шаг 4. Задаем k=0.

Шаг 5. Проверяем условие k ≤ n – 1;

а) если k ≤ n – 1, то переходим к шагу 6;

б) если k = n, то полагаем j = j + 1 и переходим к шагу 3.

Шаг 6. Вычисляем Ñf(x^jk).

Шаг 7. Проверить выполнения условия :

а) если условие выполнено, то расчет окончен и x^*=x^jk;

б) если нет, то переходим к шагу 8.

Шаг 8. Вычисляем t_k^* из условия

.

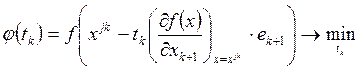Шаг 9. Вычисляем .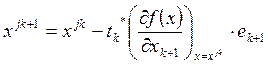

Шаг 10. Проверяем выполнение условий

,  :

а) если оба условия выполнены в двух последовательных циклах с номерами j и j – 1, то расчет окончен, найдена точка x^*=x^jk+1;

б) если не выполняется хотя бы одно условие, полагаем k=k+1 и переходим к шагу 5.

Геометрическая интерпретация метода для n=2 приведена на рисунок