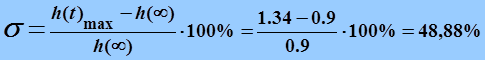Пример выполнения курсовой работы с помощью ЭВМ, страница 4

;

      Должно быть,следовательно, у нас не очень  хорошее перерегулирование, так как превышает заданное значение ;

¨  Степень затухания – для колебательных систем (это про нас):

;

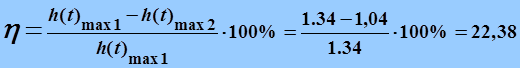      Должно быть , степень затухания также не удовлетворяет условию;

¨  Логарифмический декремент затухания :

.

«Оглавление»

2*  Синтез методом логарифмических частотных характеристик

2.1* Построение логарифмических амплитудно-частотных характеристик элементов

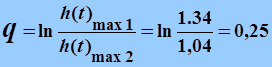      Генератор представляет собой инерционное звено первого порядка. Его асимптотическая логарифмическая амплитудно-частотная характеристика представлена на рисунке 2.1 

 

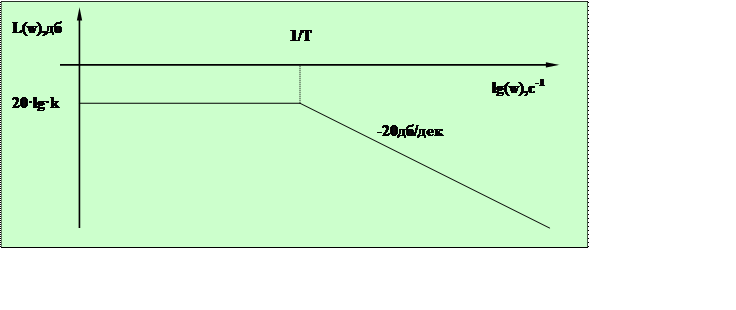Рисунок 2.1- Логарифмическая амплитудно-частотная характеристика генератора

Ее параметры определяются из передаточной функции

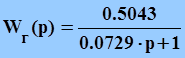
Частота сопряжения:

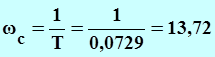, (Гц),

Амплитуда:

, ( дб)

     Для построения логарифмической амплитудно- частотной характеристики двигателя, необходимо проверить выполнение условия:

     По данным передаточной функции двигателя

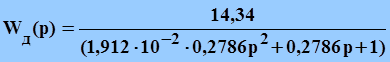
получается

то есть

     Следовательно данная передаточная функция является инерционным звеном второго порядка. Асимптотическая логарифмическая амплитудно-частотная характеристика имеет следующий вид (рисунок 2.2)

 

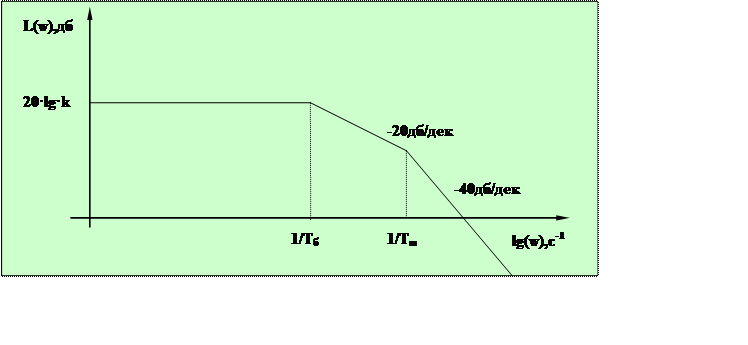Рисунок 2.2 -Логарифмическая амплитудно-частотная характеристика двигателя

Частота сопряжения меньшая:

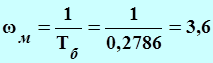, (Гц),

Частота сопряжения большая:

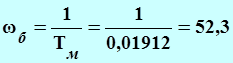, (Гц¹),

Амплитуда:

, ( дб)

Тахогенератор представляет собой пропорциональное звено, логарифмическая амплитудно-частотная характеристика которого представлена на рисунке 2.3

 

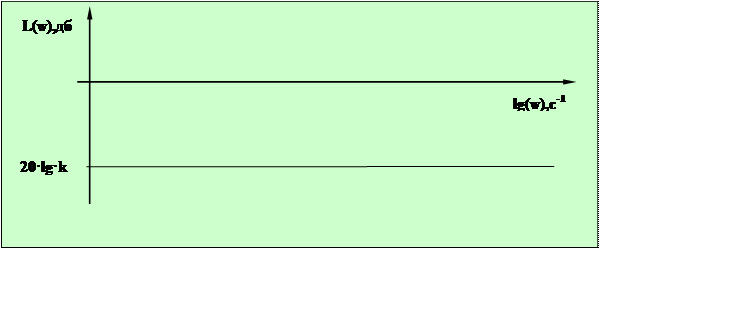Рисунок 2.3 - Логарифмическая амплитудно-частотная характеристика тахогенератора

Передаточная функция тахогенератора:

Амплитуда:

, ( дб)

      Звено предварительной коррекции представляет собой пропорциональное звено, логарифмическая амплитудно-частотная характеристика которого представлена на рисунке 2.4

 

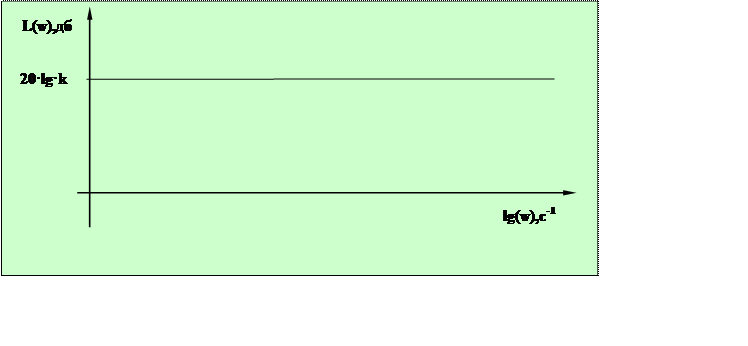Рисунок 2.4 – Логарифмическая амплитудно-частотная характеристика звена предварительной коррекции

Передаточная функция звена предварительной коррекции:

Амплитуда:

, ( дб)

«Оглавление»

2.2* Построение логарифмической амплитудно-частотной характеристики разомкнутой системы

     Так как генератор, двигатель, тахогенератор включены последовательно, то логарифмическая амплитудно-частотная характеристика разомкнутой некорректированной  системы находится как сумма трех характеристик, то есть:

Ее построение приведено на рисунке 2.5

 

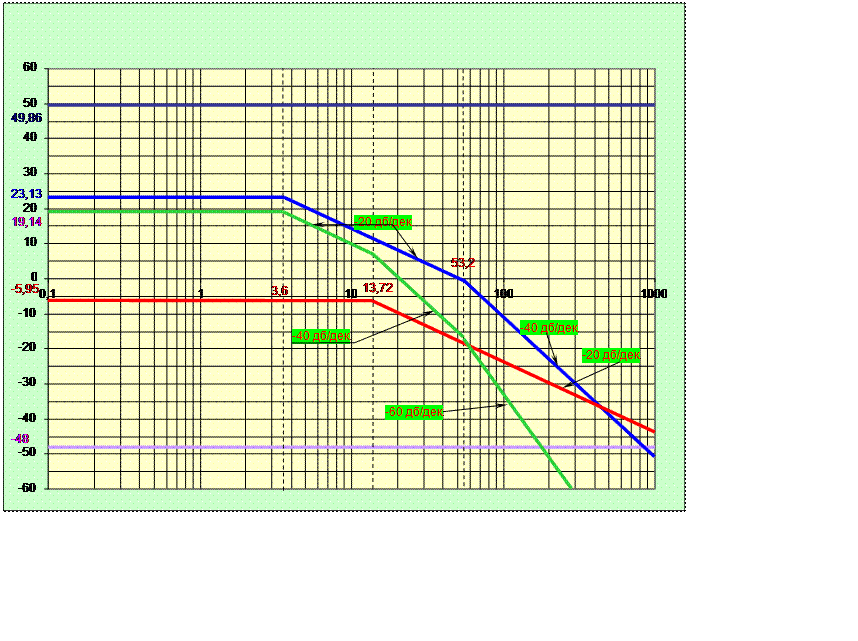
Рисунок 2.3 –Построение логарифмической амплитудно-частотной характеристики некорректированной системы

«Оглавление»

2.3 *Построение желаемой логарифмической амплитудно-частотной характеристики

Желаемая логарифмическая амплитудно-частотная характеристика состоит из трех участков: низких, средних и высоких частот.

     Для построения участка низких частот необходимо знать коэффициент системы, который находится из выражения:

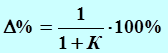
так как по заданию статическая точность системы в процентах равна .

Тогда

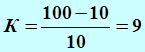_, (В);,

Для статических систем участок низких частот представляют собой параллельную оси частот и отстоящую от нее на величину  

(рисунок 2.6)

 

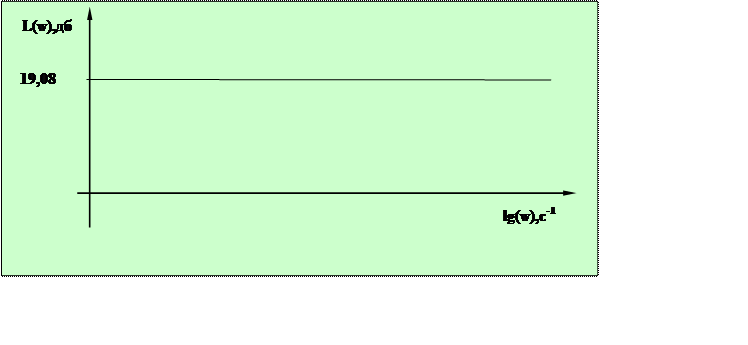Рисунок 2.6 –Участок низких частот

     Логарифмическая амплитудно-частотная характеристика на участке средних  частот представляют собой прямую с наклоном  проходящую через частоту среза.

     Этот участок ограничен запасом устойчивости по амплитуде , который определяется по круговым диаграммам в логарифмическом масштабе.

Частота среза определяется по номограмме [2[БММ12] [БММ13] ][БММ14]  при перерегулировании

 ,

получается

,

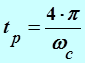или

,

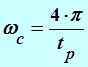     При заданном , будет

 (сек),

     По этой же номограмме определяется