4. Лабораторная работа № 3
ИССЛЕДОВАНИЕ ДЕЛИТЕЛЕЙ НАПРЯЖЕНИЯ
Цель работы: изучить характеристики резистивных делителей напряжения при различных нагрузках, научиться измерять коэффициент передачи четырехполюсника с помощью электронно-лучевого осциллографа.
В общем случае периодически изменяющиеся электрические величины (напряжения, токи, ЭДС) характеризуются мгновенными, максимальными (амплитудными) и действующими значениями. Значение электрической величины в произвольный момент времени называют мгновенным. Мгновенные значения являются величинами переменными, т. е. зависят от времени. При гармонических воздействиях мгновенные значения тока и напряжения определяют из выражений
![]() ;
; ![]() .
.
Максимальным (амплитудным) называют наибольшее из мгновенных значений за период. У гармонических напряжений и токов амплитудное значение есть величина постоянная, не зависящая от времени. Действующим значением периодического переменного тока (напряжения, ЭДС) является такой постоянный ток, при котором в той же нагрузке за время, равное периоду, выделяется такая же энергия, как и при данном переменном токе. Действующее значение напряжения (тока) есть величина постоянная. Отношение действующего значения к амплитудному зависит от формы сигнала. У гармонических сигналов U/Um = 0,707. Максимальное (Um), действующее (U) значения и размах напряжения (Up ) связаны между собой постоянными коэффициентами, а следовательно, являются пропорциональными величинами. Например, для гармонических сигналов Um :Up :U= 1: 2: 0,707. Если цепь состоит из чисто резистивных элементов и питается от источника с постоянной во времени ЭДС, то отклики (токи в ветвях и напряжения на участках цепи) пропорциональны воздействию. Так как действующее, амплитудное значения и размах напряжения при гармонических сигналах также не зависят от времени, как и при постоянном токе, а в резистивных цепях отсутствуют сдвиги фаз между напряжениями и токами, то рассчитывать отклики в таких цепях можно для Рис. 2.1 этих параметров по тем же формулам, по которым они определялись в цепях постоянного тока.

Рис. 2.1
При анализе цепей на переменном токе вводят понятие положительного направления тока, причем если направление тока в цепи совпадает с выбранным положительным, то такой ток имеет знак плюс, а если противоположное, то минус.
Цепи, имеющие две пары внешних зажимов, называют четырехполюсниками. У четырехполюсников различают входные и выходные зажимы (рис. 2.1). Коэффициент передачи цепи по напряжению
К
=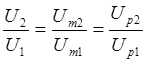 .
.
Коэффициент передачи К (для краткости слова “по напряжению” в дальнейшем тексте будем опускать) является важнейшей характеристикой цепи, так как дает возможность рассчитать напряжение на выходе по известному напряжению на входе. Очевидно, что
U2=KU1; Um2=KUm1; Up2=KUp1.
(Для краткости все последующие выкладки будем производить для действующих значений, хотя с равным успехом их можно было бы производить и для максимальных значений и для размаха.) Коэффициент передачи любой линейной цепи не зависит от входного напряжения и определяется только параметрами элементов, из которых собрана цепь, а также способа их соединения. Чтобы рассчитать в линейной цепи коэффициент передачи, необходимо:
1) задаться произвольным напряжением на входе U1;
2) любым методом вычислить напряжение на выходе U2;
3) найти отношение U2/U1, (входное напряжение в расчетной формуле при этом сократится).
Получившееся выражение не зависит от входного напряжения U1, и является коэффициентом передачи цепи. Аналогичным образом можно определить коэффициент передачи по току
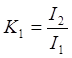
или по мощности
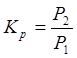 .
.
Частные случаи.
l. Рассчитаем
коэффициент передачи Г-образного четырехполюсника при холостом ходе на выходе (рис. 2.2) Для этого зададимся напряжением на входе U1, тогда действующее значение тока в цепи 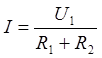 , действующее значение напряжения на выходе
, действующее значение напряжения на выходе
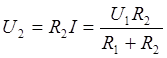 , коэффициент передачи
, коэффициент передачи 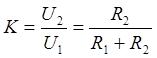 .
.
В
Г-образных четырехполюсниках коэффициент передачи равен отношению выходного
сопротивлений четырехполюсника R2 к входному R1+R2; 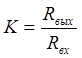 .
Входным сопротивлением четырехполюсника называют сопротивление между входными,
а выходным — между выходными зажимами цепи. Выражение
.
Входным сопротивлением четырехполюсника называют сопротивление между входными,
а выходным — между выходными зажимами цепи. Выражение 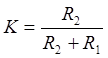 справедливо
только для четырехполюсников вида рис. 2.2.
для четырехполюсников иного вида рассчитывать коэффициент передачи следует по
общему правилу.
справедливо
только для четырехполюсников вида рис. 2.2.
для четырехполюсников иного вида рассчитывать коэффициент передачи следует по
общему правилу.
2.
Вычислим коэффициент передачи К для мостовой цепи в режиме холостого хода на
выходе, т. е. при разомкнутых вторичных зажимах (рис.
2.3). Зададимся входным напряжением U1 . В этом случае через
резисторы R1 и R4 протекает ток 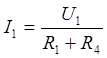 , а через R2 и R3—
ток
, а через R2 и R3—
ток 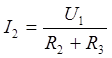 . Примем потенциал точки F за
нулевой.
. Примем потенциал точки F за
нулевой.
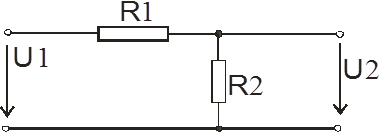
Рис. 2.2
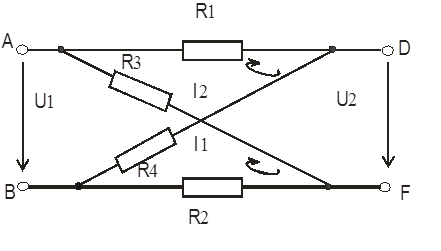
Рис. 2.3
Если
положительное направление тока такое, как показано на рис.
2.3, то потенциал точки А выше потенциала точки F на падение
напряжения на резисторе R3 (поскольку при указанном положительном
направлении напряжения источника U1 ток течет от точки А к точке F),
т. е. 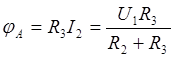 . Так как через резистор R1 ток
течет от точки А к точке D, то
потенциал точки D ниже потенциала точки А на падение напряжения на резисторе
R1, т. е.
. Так как через резистор R1 ток
течет от точки А к точке D, то
потенциал точки D ниже потенциала точки А на падение напряжения на резисторе
R1, т. е.
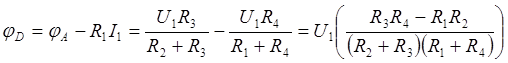
Выходное напряжение
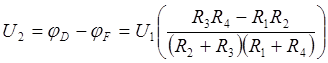 (2.1)
(2.1)
Коэффициент
передачи 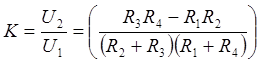
Из последнего выражения следует, что коэффициент передачи цепи зависит только от параметров цепи и не зависит от приложенного к ней напряжения.
Исследуем,
каким образом изменяется коэффициент передачи данного четырехполюсника, если
сопротивления R1, R2, R4 постоянны, а сопротивление R3 изменяется от 0 до ![]() . При R3 = 0
. При R3 = 0 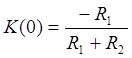 . Если в выражение
(2.1) подставим R3=
. Если в выражение
(2.1) подставим R3=![]() то получим неопределенность вида
то получим неопределенность вида ![]() . Чтобы избавиться от неопределенности,
вынесем из числителя и знаменателя множитель R3:
. Чтобы избавиться от неопределенности,
вынесем из числителя и знаменателя множитель R3:
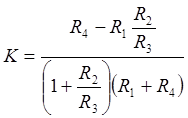
При R3=![]() К(
К(![]() ) =
) = 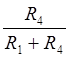 . Таким образом. в цепи рис. 2.3 при
изменении R3 на от 0 до
. Таким образом. в цепи рис. 2.3 при
изменении R3 на от 0 до ![]() коэффициент
передачи К изменяется от -
коэффициент
передачи К изменяется от -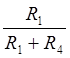 до
до 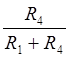 (рис. 2.4).
(рис. 2.4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.