Инвариантные системы. Условие инвариантности для систем стабилизации. Условие инвариантности для следящей системы

Инвариантные системы

Из словаря: инвариантность – это неизменность.

В автоматике: автоматическая системы, в которой любая выходная величина (в том числе сигнал ошибки) не зависит от внешнего возмущения, называется инвариантной. То есть это независимость одной физической величины от другой.

Задача всех АСР – точно воспроизводить задание на выходе. В статическом режиме точность можно повысить увеличивая порядок астатизма nи коэффициент передачи К. Но увеличение коэффициента передачи K ведет к уменьшению запаса устойчивости и увеличению колебательности, следовательно, ухудшается точность в переходном режиме.

Это противоречие можно решить путем введения управляющего воздействия по возмущению z(t).

Системы, у которых используются два принципа управления: по отклонению и по возмущению, называются комбинированными (рис.1).

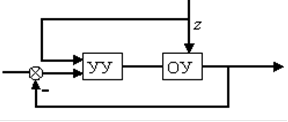
Рис. 1

Для систем стабилизации (рис.2) инвариантность заключается в следующем: необходимо добиться независимости выходной величины от возмущающего воздействия.

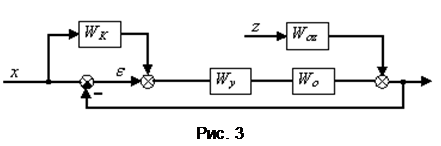
В следящих системах (рис.3) – необходимо добиться независимости сигнала ошибки от задающего воздействия.

Математические расчеты условий такой независимости называется теорией инвариантности.

Практическая ценность: в системах с выполнением условий инвариантности возрастает прикладная значимость

В первые идею инвариантности высказал Щипанов (1938 г.). Актуальность проблемы инвариантности приравнивается к актуальности устойчивости.

Первое решение – использование комбинированного управления: необходимо измерить возмущение z(t) и организовать новый канал управления на объект.

Условие инвариантности для систем стабилизации

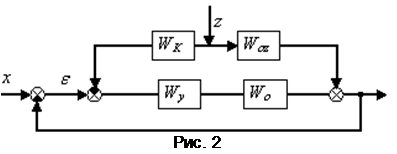
W_o –передаточная функция ОУ по задающему воздействию

W_oz - передаточная функция по возмущению

W_y - передаточная функция управляющего устройства

W_К - передаточная функция компенсирующего устройства

Задача: надо найти W_К.

Найдем передаточную функцию по каналу возмущения:

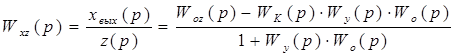.                                        (1)

Найдем передаточную функцию по заданию:

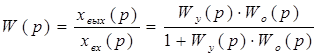.                                                 (2)

Независимость выходной величины от возмущения z(t) будет, если W_xz(p)=0, тогда из уравнения (1) получаем условие инвариантности: 

или

.

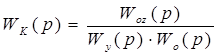Чтобы добиться компенсации в установившимся режиме нужен усилитель с коэффициентом усиления К_ус:

.

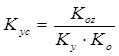W_y(p) – должна иметь вид дробно-рациональной функции, в которой максимальная степень числителя должна быть меньше либо равна максимальной степени знаменателя (с точки зрения физической реализации).

Условие инвариантности для следящей системы

Требуется обеспечить независимость сигнала ошибки e(t) от задающего воздействия x_вх(t).

Найдем передаточную функцию относительно ошибки:

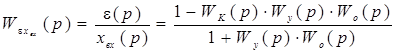
Отсюда находим условие инвариантности:

или

 .

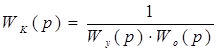Но полученная передаточная функция W_к(р) физически не реализуема, т.к. порядок  полинома числителя больше порядка полинома знаменателя.

            Таким образом инвариантность – это дополнительное свойство системы, его создают искусственно для удовлетворения специальных требований. Реализуют инвариантность за счет: 1) усиления энергетических возможностей; 2) прямого или косвенного измерения возмущения, в результате чего создается компенсирующее воздействие.

В результате реализации условий инвариантности легче решаются проблемы: точности, оптимальности, быстродействия, помехозащищённости.

            Но сама по себе инвариантность непостоянна, требуется постоянный контроль и автоматизация на базе принципов адаптации.