


Федеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт цветных металлов и материаловедения
Кафедра автоматизации производственных процессов
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1
Вариант 2
Преподаватель Г.Б. Даныкина
Студент МФ 07-08 И.В. Большаков
Красноярск 2011
Цель работы: изучить методы решения задач линейного программирования; приобрести навыки разработки моделей линейного программирования и решения задач на ЭВМ.
Исходные данные для выполнения работы приведены в таблице 1.
Таблица 1 – Исходные данные
|
Вариант |
Критерий |
Ограничения |
|
2 |
–2·x1 + 3·x2 → max |
x1 + 2·x2 ≤ 12 3·x1 + 2·x2 ≥ 8 –2·x1 + x2 ≥ –8 |
1 Решение графическим методом
Выразим x2 из условий ограничений:
1) x1 + 2·x2 ≤ 12 2) 3·x1 + 2·x2 ≥ 8 3) –2·x1 + x2 ≥ –8
x2 = 6 – 0,5·x x2 = 4 – 1,5·x1 x2 = 2·x1 – 8
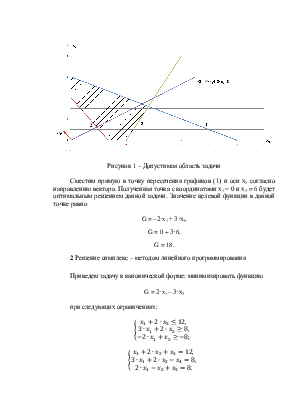
Задаваясь значениями x1 построим графики ограничений (рисунок 1)
|
x1 |
0 |
12 |
x1 |
0 |
2 |
x1 |
4 |
8 |
||
|
x2 |
6 |
0 |
x2 |
4 |
1 |
x2 |
0 |
8 |
Построим график целевой функции G (рисунок 1) и определим ее градиент. Для этого приравняем выражение x1 + 3·x2 к константе и выразим x2.
–2·x1 + 3·x2 = 0,
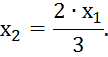
|
x1 |
0 |
9 |
|
x2 |
0 |
6 |
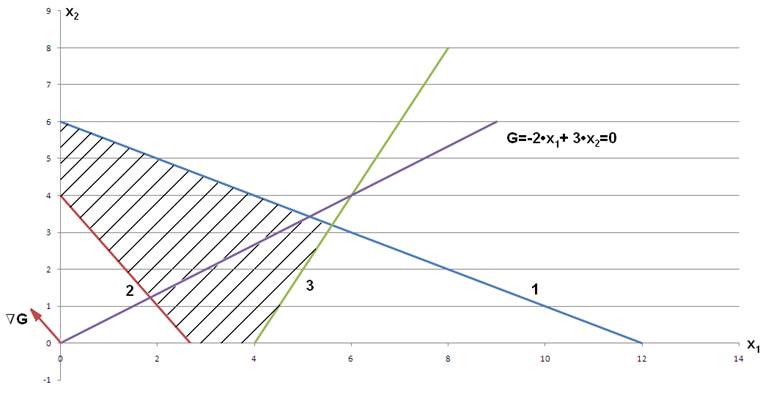
Рисунок 1 – Допустимая область задачи
Сместим прямую в точку пересечения графиков (1) и оси х2 согласно направлению вектора. Полученная точка с координатами х1 = 0 и х2 = 6 будет оптимальным решением данной задачи. Значение целевой функции в данной точке равно
G = –2·x1 + 3·x2,
G = 0 + 3·6,
G = 18.
2 Решение симплекс – методом линейного программирования
Приведем задачу к канонической форме: минимизировать функцию
G = 2·x1 – 3·x2
при следующих ограничениях:
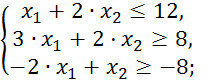
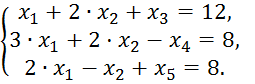
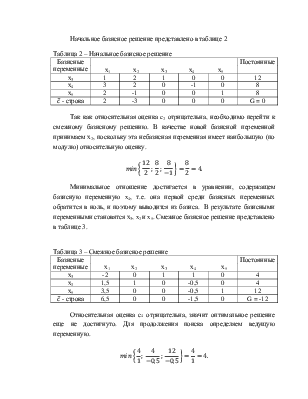
Начальное базисное решение представлено в таблице 2
Таблица 2 – Начальное базисное решение
|
Базисные переменные |
Постоянные |
|||||
|
х1 х2 х3 х4 х5 |
||||||
|
х3 |
1 |
2 |
1 |
0 |
0 |
12 |
|
х4 |
3 |
2 |
0 |
-1 |
0 |
8 |
|
х5 |
2 |
-1 |
0 |
0 |
1 |
8 |
|
|
2 |
-3 |
0 |
0 |
0 |
G = 0 |
Так как относительная оценка c2 отрицательна, необходимо перейти к смежному базисному решению. В качестве новой базисной переменной принимаем x2, поскольку эта небазисная переменная имеет наибольшую (по модулю) относительную оценку.
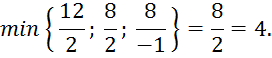
Минимальное отношение достигается в уравнении, содержащем базисную переменную x4, т.е. она первой среди базисных переменных обратится в ноль, и поэтому выводится из базиса. В результате базисными переменными становятся x3, x2 и x5. Смежное базисное решение представлено в таблице 3.
Таблица 3 – Смежное базисное решение
|
Базисные переменные |
Постоянные |
|||||
|
х1 х2 х3 х4 х5 |
||||||
|
х3 |
-2 |
0 |
1 |
1 |
0 |
4 |
|
х2 |
1,5 |
1 |
0 |
-0,5 |
0 |
4 |
|
х5 |
3,5 |
0 |
0 |
-0,5 |
1 |
12 |
|
|
6,5 |
0 |
0 |
-1,5 |
0 |
G = -12 |
Относительная оценка c4 отрицательна, значит оптимальное решение еще не достигнуто. Для продолжения поиска определяем ведущую переменную.
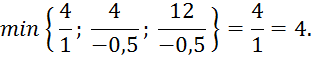
Минимальное отношение достигается в уравнении, содержащем базисную переменную x3, т.е. она первой среди базисных переменных обратится в нуль, и поэтому выводится из базиса. В результате базисными переменными становятся x4, x2 и x5. Второе смежное базисное решение представлено в таблице 4.
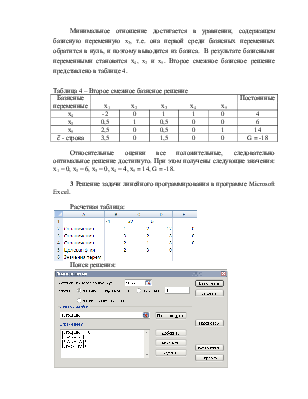
Таблица 4 – Второе смежное базисное решение
|
Базисные переменные |
Постоянные |
|||||
|
х1 х2 х3 х4 х5 |
||||||
|
х4 |
-2 |
0 |
1 |
1 |
0 |
4 |
|
х2 |
0,5 |
1 |
0,5 |
0 |
0 |
6 |
|
х5 |
2,5 |
0 |
0,5 |
0 |
1 |
14 |
|
|
3,5 |
0 |
1,5 |
0 |
0 |
G = -18 |
Относительные оценки все положительные, следовательно оптимальное решение достигнуто. При этом получены следующие значения: х1 = 0, х2 = 6, х3 = 0, х4 = 4, х5 = 14, G = -18.
3 Решение задачи линейного программирования в программе Microsoft Excel.
Расчетная таблица:
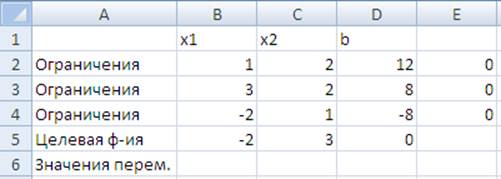
Поиск решения:
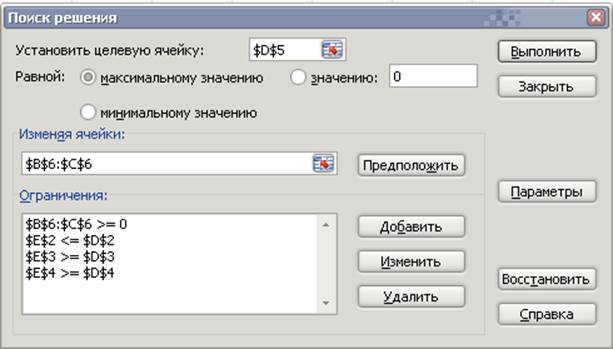
Параметры поиска решения:
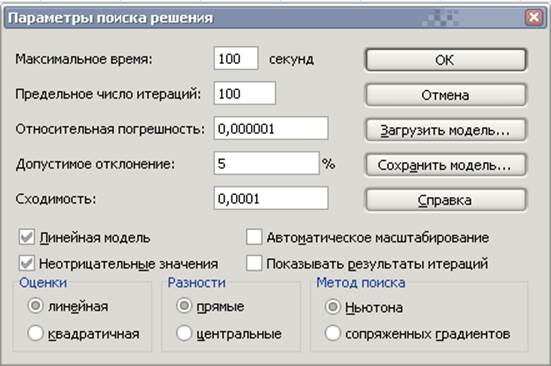
Полученное оптимальное решение:
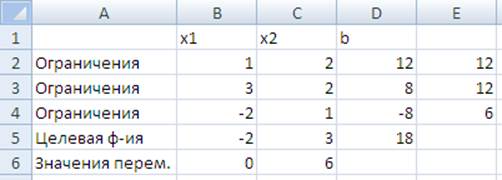
То есть: х1 = 0, х2 = 6 и G = 18.
Вывод: Изучили методы решения задач линейного программирования, результаты по всем 3-м способам совпали, следовательно, все шаги были выполнено верно и оптимальным решением данной задачи является значения х1 = 0, х2 = 6 и при этом критерий оптимальности G = 18.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.