

Билет 26
Вопрос 1.
Бесконечно большие функции.

Опр.4.4.8. Функцияf(x) называется бесконечно большой при х®а, если ![]() .
.
Обозначение: ![]() .
.
Опр.4.4.9. Функцияf(x) называется положительной бесконечно большой при х®а, если ![]() .
.
Опр.4.4.9. Функцияf(x) называется отрицательной бесконечно большой при х®а, если ![]() .
.
А)связь между б.б.ф и б.м.ф

Теор. 4.4.11.1 о связи ББ и
БМ функций. Пусть функции F(x) и j(x) связаны соотношением F(x)= .
F(x)
- ББ тогда и только тогда, когда j(x) -БМ.
.
F(x)
- ББ тогда и только тогда, когда j(x) -БМ.
Док-во. Необходимость. Пусть F(x) - ББ,
докажем, что 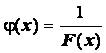 - БМ. Возьмём "e>0. По определению ББ, для М=1/e $d: 0<| x-a |<dÞ| F(x) |> М. Тогда
- БМ. Возьмём "e>0. По определению ББ, для М=1/e $d: 0<| x-a |<dÞ| F(x) |> М. Тогда 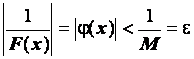 , т.е. j(x) удовлетворяет
определению БМ.
, т.е. j(x) удовлетворяет
определению БМ.
Достаточность доказывается аналогично необходимости.
Итак, связь между ББ и БМ функциями достаточно простая. Поэтому кратко перечислим факты, относящиеся к сравнению ББ функций и аналогичные определениям и теоремам для БМ.
Вопрос 2.
Теоремы Лопиталя.

Теор.7.5 (неопределённость
![]() ). Пусть функции f (х) и g
(х):
). Пусть функции f (х) и g
(х):
1. непрерывны на отрезке [a, b];
2.![]() ,
, ![]() ;
;
3. существуют производные f '(х) и g'(х) на интервале (a,b), причём g'(х) ¹ 0;
4. существует (конечный или бесконечный) 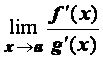 . Тогда существует
. Тогда существует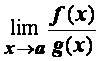 , и
, и 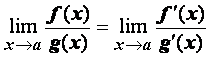 .
.
 Док-во. Так как функции f
(х) и g (х)
непрерывны в точке а, то
Док-во. Так как функции f
(х) и g (х)
непрерывны в точке а, то 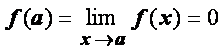 ,
,
![]() , и
, и 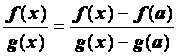 . Для функций f
(х) и g (х)
на отрезке [a, х]
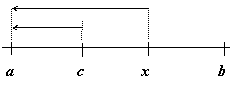
выполняются условия теоремы Коши, поэтому существует точка сÎ(a,
х), такая что
. Для функций f
(х) и g (х)
на отрезке [a, х]
выполняются условия теоремы Коши, поэтому существует точка сÎ(a,
х), такая что 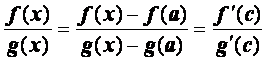 .
Устремим
.
Устремим ![]() , при этом и
, при этом и ![]() . В пределе получим
. В пределе получим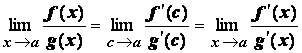 , что и требовалось доказать.
, что и требовалось доказать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.