Построение переходных процессов в ИС. Построение переходных процессов по разложению z-преобразованием в степенной ряд

Построение переходных процессов в ИС

Динамические свойства  ИС можно охарактеризовать с помощью переходной характеристики β[n,ε] и импульсной переходной (весовой) k_р[n,ε], обе эти характеристики имеют тот же физический смысл, что h(t) и ω(t) для непрерывных систем.

Переходная  функция может быть найдена по реакции системы на дискретное единичное воздействие на входе.

Дискретные значения весовой функции определяются реакцией системы на единичный импульс на ее входе.

Переходная функция β[n,ε] замкнутой ИС может быть построена  по ее дискретным изображениям. Изображение переходной функции β^*(q,ε) найдем из К_р^*(q,ε) .

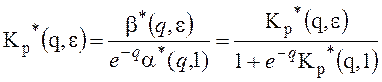
Т.к. рассматриваем вопрос нахождения переходной функции то на вход подается единичное ступенчатое воздействие 1[n], для которой

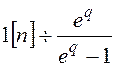  тогда

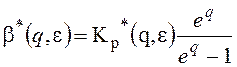
Или относительно z-преобразования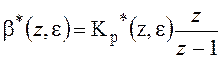

Задача: необходимо найти β[n,ε] решая переходную функцию по ее дискретному изображению.

Существует 3 способа:

1. Нахождение β[n,ε] непосредственно по изображению β^*(q,ε), используя таблицы дискретного преобразования Лапласа. Этот способ удобен, если изображение переходной функции представлено в табличном виде (см. практику).
2. Состоит в разложении изображения переходной функции β^*(q,ε) в степенной ряд по степени (z^k).
3. Нахождение переходной функции β[n,ε] на основании разностных уравнений.

Построение переходных процессов

по разложению z-преобразованием β^*(z,ε) в степенной ряд

(2-й способ)

Изображение переходной функции определяется по выражению

или для единичного ступенчатого воздействия

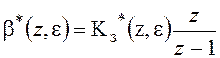                                                                (1)

В общем виде изображение переходной функции можно представить в виде полиномов

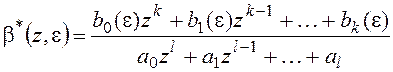,    где k ≤ l                                  (2)

Пользуясь формулой z преобразования можно записать:

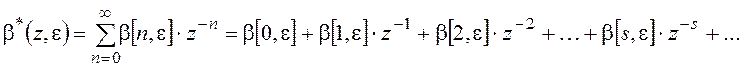         (3)

В выражении (3) коэффициенты при соответственных степенях z равны значениям переходной  функции в конкретные моменты времени.

Чтобы найти β[n,ε] надо найти коэффициенты при соответственных степенях z. Для этого поделим уравнение (2) на z^l.

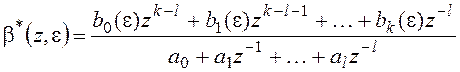
Вынесем общий множитель z^k-l

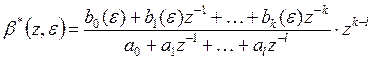                                             (4)

Приравниваем правые части уравнений (3) и (4)

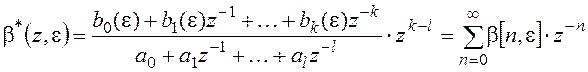
Переносим z^k-l в правую часть

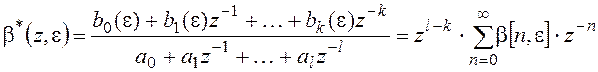                        (5)

По теореме опережения дискретного преобразования Лапласа можно записать:

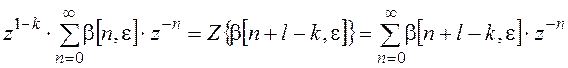
Тогда уравнение (5) будет

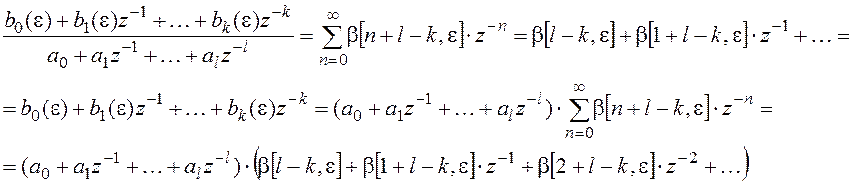
Находим коэффициенты при соответственных степенях z:

Из этих выражений выделяем β:

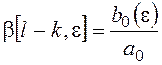
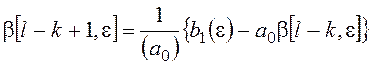
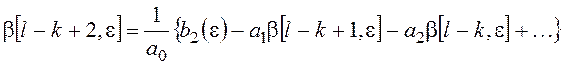
В результате получим:

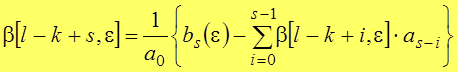                                        (6)

Пользуясь выражением (6) можно рассчитать последовательно дискретные значения переходной функции,  начиная с момента времени l-k, т.е. первое расчетное значение будет β[l-k,ε], до этого времени переходная функция равна 0. Здесь l степень полинома знаменателя изображения переходной функции β^*(q,ε), а k – числителя (уравнение (2)), где k≤l. Если k=l, то первое расчетное значение β[0,ε].