Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам разомкнутой системы: Методические указания по курсу «Теория автоматического управления»

Государственный университет цветных металлов и золота

Кафедра:  Автоматизация производственных процессов

Построение вещественной частотной характеристики замкнутой системы по частотным характеристикам

разомкнутой системы

Методические указания по курсу

 «Теория автоматического управления»

для самостоятельной работы студентов специальности 220301(210200)

«Автоматизация технологических процессов

и производств (по отраслям)»

Рассмотрено на заседании

кафедры АПП

______________________

Протокол №___________

Красноярск, 2005

Построение вещественной частотной характеристики замкнутой системы P_з(w) по частотным характеристикам разомкнутой системы

Построение вещественной частотной характеристики замкнутой системы требует довольно трудоемких вычислений. При исследовании устойчивости системы часто вычерчивается амплитудно-фазовая характеристика (АФХ) или логарифмические частотные характеристики (ЛЧХ) разомкнутой системы. Разработаны методы построения вещественной частотной характеристики (ВЧХ) замкнутой системы по уже имеющимся АФХ и ЛЧХ разомкнутой системы, которые могут быть получены теоретически и экспериментально.

В.В.Солодников предложил метод графического построения ВЧХ замкнутой системы по готовой амплитудно-фазовой  характеристики разомкнутой системы. Метод можно применять, если:

1) система является минимально-фазовой,

2) при возмущающем воздействии в виде единичного скачка,

3) при нулевых начальных условиях,

4) когда передаточная функция замкнутой системы имеет вид:

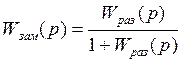                        ,                               (1)

где W_раз(р) – передаточная функция разомкнутой системы.

Такой вид имеют передаточные функции подавляющего большинства замкнутых систем автоматического регулирования.

Минимально-фазовыми называются системы автоматического регулирования, передаточные функции которых не имеют нулей (корни многочлена в числителе) и полюсов (корни характеристического уравнения, находящегося в знаменателе), расположенных в правой полуплоскости комплексной плоскости.

В минимально-фазовых системах сдвиг фазы выходной величины по отношению к входной оказывается при всех частотах наименьшим из всех возможных для данной амплитудной характеристики.

Например, система с передаточной функцией

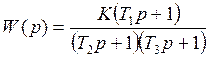
является минимально-фазовой, а система с передаточной функцией

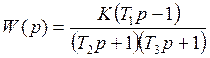
является неминимально-фазовой. Обе эти системы имеют одинаковые АЧХ. Но у первой системы максимальный сдвиг между входом и выходом при  ω→∞ cоставляет минус 90⁰, а у второй, которая имеет нуль (корень числителя), расположенный в правой полуплоскости, фазовый сдвиг при ω→∞ cоставляет минус 270⁰.

У минимально-фазовых систем между амплитудной и фазовой характеристиками существует однозначная зависимость. Если задана одна характеристика, то, в принципе, можно найти другую. У неминимально-фазовых систем такой однозначной зависимости между характеристиками нет. На практике приходится иметь дело с устойчивыми  минимально- фазовыми системами автоматического регулирования.

1. Построение ВЧХ по АЧХ разомкнутой системы

Заменяя в выражении (1) p=jω, найдем амплитудно–фазовой характеристику замкнутой системы

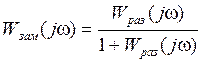                                     .                          (2)

Отделим в амплитудно–фазовых характеристиках замкнутой и разомкнутой систем вещественную и мнимую части:

                                                            (3)

Подставив эти значения в выражение (2), получим:

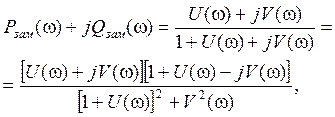
откуда выделяем вещественную часть замкнутой системы

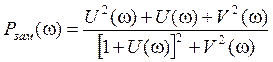.                       (4)

Пользуясь выражением (4) на готовой АФХ разомкнутой системы для каждой частоты ω_i последовательно снимают значения U(ω_i) и V(ω_i), рассчитывают Р_зам(ω_i) и строят ВЧХ замкнутой системы.

2. Построение ВЧХ по круговым диаграммам

Преобразуем выражение (4)

,

 откуда

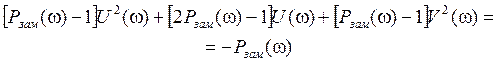
 или

.

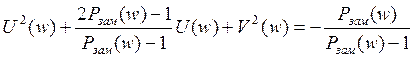Прибавим к правой и левой частям величину

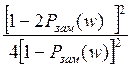
и после преобразования получим

                                   (5)                  

где

        

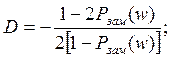
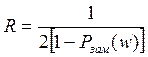
Для различных постоянных значений P_зам(w) выражение (8) представляет уравнение окружностей с радиусом R, центры которых лежат на вещественной оси на расстоянии D от начала координат.

Во всех случаях

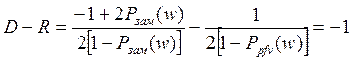                                         ,                   (6)

что свидетельствует о том, что все окружности для различных значений P_зам(w) проходят через точку (-1; j0).

Семейство окружностей для различных значений P_зам(ω), построенных на плоскости U, j, V, приведено на рисунке 2. Здесь цифры, помещенные в разрыве окружностей и называемые индексами, являются ординатами ВЧХ замкнутой системы. Если на этой плоскости построить амплитудно-фазовую характеристику разомкнутой системы, то точка пересечения этой характеристики с окружностью дает координаты вещественной частотной характеристики: ордината P_зам(ω_i) равна индексу окружности, а частота ω_i – частоте, соответствующей точке пересечения АФХ с окружностью.

Рис. 2

На практике для построения ВЧХ замкнутой системы на круговую диаграмму (рисунок 2) накладывают кривую W(jω) (АФЧХ разомкнутой системы), выполненную в том же масштабе. Затем считывают значения Р_зам(ω), которые соответствуют индексам окружностей сетки, пересекающих кривую АФЧХ в точках, соответствующих частотам ω_i.

Находя координаты по каждому пересечению амплитудно–фазовой характеристики с различными окружностями, строим вещественную частотную характеристику.

3. Построение ВЧХ по логарифмическим частотным характеристикам

Вещественная частотная характеристика замкнутой системы может быть построена также по логарифмическим частотным характеристикам разомкнутой системы с помощью диаграммы, приведенной на рисунке 3. По оси абсцисс отложены значения фазы в градусах, а по оси ординат – значения отношения амплитуд в децибелах. В этих координатах построены кривые, соответствующие окружностям на рисунке 2. Цифры, стоящие у каждой кривой, которые тоже называются индексами, представляют ординаты вещественной частотной характеристики замкнутой системы.

Рис. 3

По имеющимся логарифмическим частотным характеристикам определяем фазы и отношения амплитуд для соответственно одинаковых частот и наносим эти точки на диаграмму (рис. 3). Соединив эти точки плавной кривой, получаем амплитудно-фазовую характеристику разомкнутой системы в логарифмическом масштабе. В точках пересечения этой характеристики с кривыми по индексу кривой определяем ординату вещественной частотной характеристики замкнутой системы, которой соответствует частота совпадающая с данной кривой точки амплитудно-фазовой  характеристики.

Построение ВЧХ по логарифмическим частотным хар актеристикам облегчает синтез корректирующих устройств систем автоматического регулирования.

Таким образом, по АФХ и ЛЧХ разомкнутой системы можно построить ВЧХ замкнутой системы, а по ней – частотными методами переходную характеристику замкнутой системы.

Частотный метод рекомендуется при порядке характеристического уравнения выше третьего. Для систем до третьего порядка включительно переходной процесс достаточно просто рассчитывается на основе определения корней характеристического уравнения.

Литература

1. Иванов А.А. Теория автоматического управления и регулирования. М.: Недра, 1979, 352 с.

2. Теория автоматического управления: учеб. для вузов по спец. «автоматика и телемеханика». В 2-х ч. Ч.1 Теория линейных систем автоматического управления/ Н.А. Бабаков, А.А. Воронов, А.А. Воронова и др.; Под ред. А.А. Воронова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 367 с.