Общая постановка задачи оптимизации. Численные методы поиска безусловного экстремума. Линейное программирование: симплекс-метод и его применение для решения задач оптимизации

«Методы оптимизации»

1 Общая постановка задачи оптимизации. Необходимые и достаточные условия существования безусловного экстремума функции одной и нескольких переменных.

2 Численные методы поиска безусловного экстремума: методы нулевого порядка (методы одномерной минимизации).

3 Численные методы поиска безусловного экстремума: методы первого порядка.

4 Линейное программирование: симплекс-метод и его применение для решения задач оптимизации.

1 Общая постановка задачи оптимизации. Необходимые и достаточные условия существования безусловного экстремума функции одной и нескольких переменных.

Оптимизация – это целенаправленная деятельность, которая заключается в получении наилучших результатов при соответствующих условиях.

Задача безусловной оптимизации состоит в нахождении минимума или максимума функции в отсутствие каких-либо ограничений.

Функция у=f(x) имеет локальный min (локальный max) в точке х₀, если существует некоторая положительная величина δ, при которой выполняется неравенство: /х-х₀/<δ, а также выполняется условие f(x)≥f(x₀)- для задач минимизации; f(x)≤ f(x₀)-для задач максимизации.

Функция у=f(x) имеет глобальный min в точке х^* если для всех х выполняется условие f(x)≥f(x^*), где f(x^*) –точка глобального max.

Необходимым условием существования экстремума G(x) при отсутствии ограничений на диапазон изменения переменной x могут быть получены из анализа первой производной:

 

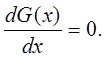Достаточные условия существования экстремума:

сравнение значений функций, сравнение знаков производных, исследование знаков высших производных.

Если G(xk-e) и G(xk+e) одновременно больше или меньше G(xk), то в точке xk – экстремум.

Если знак производной меняется при переходе через точку xk, то это экстремум. Меняется с (+) на (–), то max; с (–) на (+), то min.

Если порядок первой необращающейся в нуль в точке xk производной четный, то в данной точке есть экстремум функции G(x), который будет max или min в зависимости от знака этой производной: < 0 – max; > 0 – min.

Функция нескольких переменных G = G(x1, x2, …, xn).

Необходимое:

 

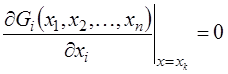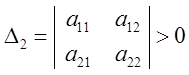Достаточное: D1 = а11 > 0;

 

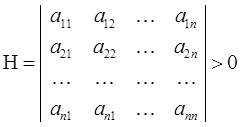
2 Численные методы поиска безусловного экстремума: методы нулевого порядка (методы одномерной минимизации).

Безградиентные методы – это методы, которые использую в процессе поиска экстремума информацию, полученную от сравнительной оценки критерия оптимальности в результате выполнения очередного шага.

Метод золотого сечения.

Задача состоит в определения положения экстремума функции одного переменного G(x) на некотором интервале [a,b]. Для решения этой задачи весь исходный интервал разбивается на части в определенном пропорциональном  отношении.

Значения функции G(x) на концах исходного интервала, в некоторых внутренних точках в точках Х₁ и Х₂ известны, выбираем один из 2-х подынтервалов [Х₀; Х₂] или [Х₁; Х₃]. В одном из этих интервалов локализуется экстремум функции G(x).

Отношение 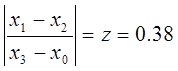, называется золотым сечением: если в интервале [Х₀; Х₃] внутренние точки Х₁ и Х₂ отстоят от концов интервала на величину z, в любом из образующихся подинтевалов можно так выбрать положение новой точки Х₄ , которая будет отстоять от концов своего подинтервала на величину z.

Одним вычислением на каждом этапе локализуем положение экстремума внутри интервала, длина которого составляет 1-z=0.62 от длины исходного интервала.

Алгоритм:

1). Вычисляем значения функции G(x) на концах исходного интервала т. е. значения G(Х₀) и G(Х₃).

2). Вычисляем значения функции в точке Х₁ = Х₀ +0,38(Х₃ - Х₀ )

3). Вычисляем значения функции в точке Х₂ = Х₃ -0,38(Х₃ - Х₀ )

4). Сравниваем полученные значения  G(Х₁) и G(Х₂) и по результатам сравнения выбирают подинтервал в котором локализуется экстремум.

Эти новые 2-а подинтервала состоят из 2-х участков l1 и l2.

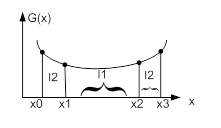
5). Внутри большого отрезка (l₁) есть точка отстоящая от концов отрезка (l₁+l₂) на 0,38. В этой точке рассчитываем значения функции G(x) и снова определяем подинтервал внутри интервала (l₁+l₂) и т. д.

Методы с использованием чисел Фибоначчи.

Свойство чисел Фибоначчи можно использовать для поиска экстремума функции одной переменной G(x). Последовательность чисел Фибоначчи: F_к = F_k-1 + F_k-2 , где F₀ = F₁ =1.

Ряд чисел Фибоначчи 1, 2,3,5,8,13,21,34,55,89

Алгоритм поиска min:

1). По заданной точности ε находим количество шагов 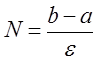, где a,b – границы интервала.

2). Для N находим из таблицы такое число для которого выполняется условие F_s-1 <N< F_s .

3). Определяем минимальный шаг поиска экстремума по найденному числу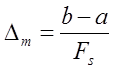

4). Считаем значения функции в точках начала и конца интервала.

 5). Определяем следующую точку из интервала, в ней считаем значение функции G(x): .

6). Рассчитываем значение функции G(x) в этой найденной новой точке G().

Сравниваем G(x) и G(). Если шаг оказался удачным G()<G(x), то определяется новая точка [a,b] по выражению: .

7). Выполняют расчет в новый точке G() и т. д. до тех пор пока шаг окажется неудачным.

В случае неудачного шага расчет новой точки выполняется по выражению например, для

8). Последующие шаги выполняются с уменьшающейся величиной шага, которую определяют по выражению: , где i=0, 1, 2,…- номер шага.

Метод дихотомии.

Дихотомия – половина деления. Из N  экспериментов находят интересующий интервал [Х₁; Х₂], Х₁ и Х₂ – это два значения отрезка, которые рассматриваются как единичный отрезок. Значения Х₁ и Х₂ располагаются симметрично относительно центра исходного интервала на расстоянии ε/2 (ε – заданная точность)

В т. Х₁ и Х₂ вычисляется значения целевой функции, и их сравнивают, определяют гарантируемый интервал неопределенности G₁=(1±ε)/2.

Допустим этот интервал неопределенности смещен влево. В результате получаем интервал отрезка между точками [0; Х₂].

Далее рассматривается отрезок [0; Х₂] внутри этого отрезка относительно центра находят новые точки Х₃ и Х₄ , которые располагаются симметрично относительно центра на величину ε/2.