






Нахождение вынужденных
симметричных колебаний
Чтобы появились автоколебания на вход системы надо вынужденно подать сигнал от генератора гармонических сигналов f(t).
Уравнение нелинейной системы:
x×Q(p)+R(p) × F(x,px)=S(p) ×f(t), (1)
где f(t) - сигнал от генератора, f(t)=B sin ωвt;
ωв - частота вынужденных колебаний,
В - амплитуда вынужденных колебаний.
Считается, что функция f(t)=B sin ωвt задана.
Решение ищем в виде: х=А (sin ωвt+φ).
С функцией F(x,px) производим гармоническую линеаризацию:
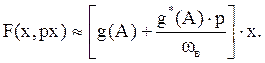
Тогда уравнение (1) будет:
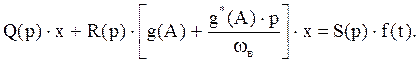
Преобразуем функцию f(t):
![]()
Из уравнения (2) выразим sin:
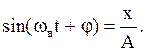
Для нахождения cos продифференцируем sin:
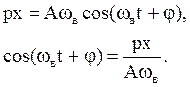
Найденные cos и sin подставляем в функцию f(t):
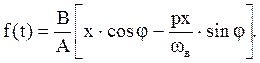
Тогда уравнение (3) будет:
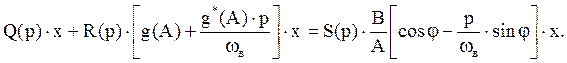
Графоаналитический способ
нахождения вынужденных симметричных колебаний
Рассматриваем уравнение
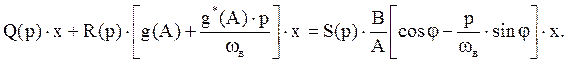
Решение х=0 не удовлетворяет, т.к. решение ищем в виде х=А (sin ωвt+φ).
Тогда рассматриваем уравнение:
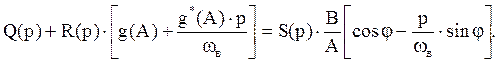
Делаем подстановку p=jωв:
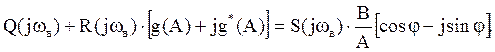
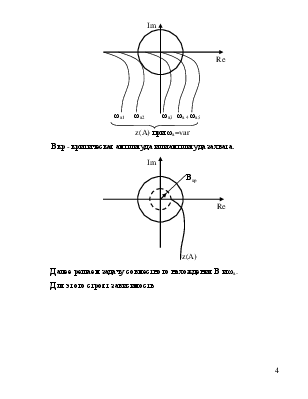
Вводим обозначение: cosφ- jsinφ=e-jφ, находим функцию z(A):
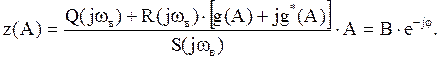
Здесь Вe-jφ - угол по окружности с радиусом r = В.
При известном В находим z(A) и φ.
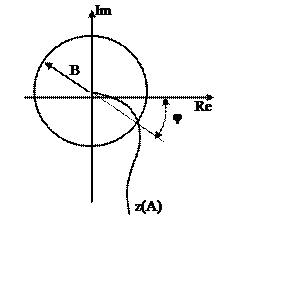
Если В<Вкр, то z(A) с окружностью пересекаться не будут, в системе автоколебания не возникают.
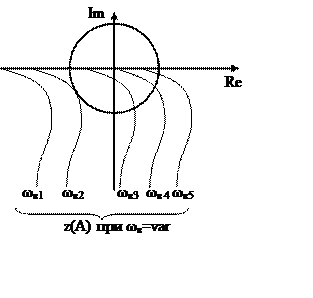
Вкр - критическая амплитуда или амплитуда захвата.

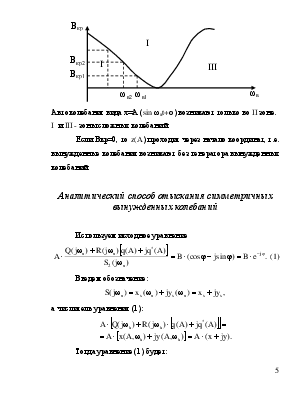
Далее решаем задачу совместного нахождения В и ωв.
Для этого строят зависимость
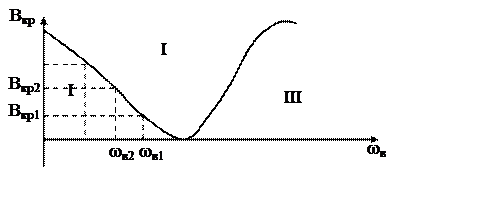
Автоколебания вида х=А (sin ωвt+φ) возникают только во II зоне. I и III - зоны сложных колебаний.
Если Вкр=0, то z(A) проходит через начало координат, т.е. вынужденные колебания возникают без генератора вынужденных колебаний
Аналитический способ отыскания симметричных вынужденных колебаний
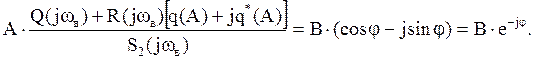 (1)
(1)
Введем обозначение:
![]()
а числитель уравнения (1):
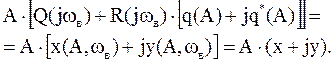
Тогда уравнение (1) будет:
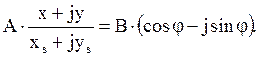
Умножим числитель и знаменатель на комплексное сопряженное знаменателю выражение:
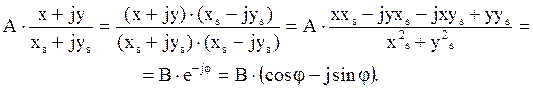
Выделяем вещественную и мнимую части, в результате получаем систему двух уравнений:
![]()
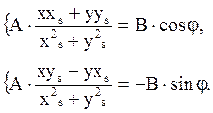
Возведем в квадрат и сложим (воспользуемся формулой cos2а + sin2а = 1):
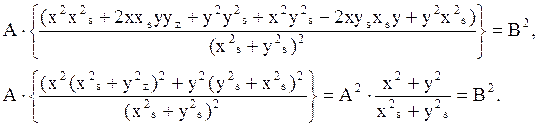 Отсюда находим А и φ:
Отсюда находим А и φ:
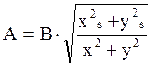 - это уравнение для нахождения А, т.к. x и y зависят от А x=f(A), y=f(A);
- это уравнение для нахождения А, т.к. x и y зависят от А x=f(A), y=f(A);
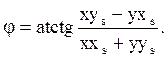
Нахождение вынужденных
несимметричных колебаний
Вынужденные несимметричные колебания могут возникнуть в системе, когда на входе действует медленно меняющаяся функция времени и если нелинейность F(x,px) несимметрична относительно начала координат.
Характеристическое уравнение системы:
![]() (1)
(1)
где f1 - медленно меняющаяся функция времени, для которой справедливо условие
![]() ,
, 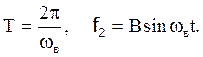
Если вынужденные колебания несимметричны, то решение ищем в виде:
x=x0+x*=x0+Asin(ωвt+φ);
где x*=Asin(ωвt+φ).
Выполним гармоническую линеаризацию с F(x,px):
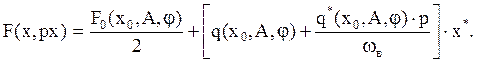
После подстановки p=jω:
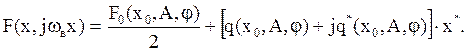
Функцию f2(t) находим как для вынужденных симметричных колебаний (добавить самостоятельно – см. выше):
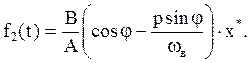
Подставляем F(x,px) и f2(t) в уравнение (1) и к полученному уравнению (добавить самостоятельно) применяем принцип суперпозиции: разбиваем его на два уравнения – для медленно меняющейся функции времени и для периодической составляющей
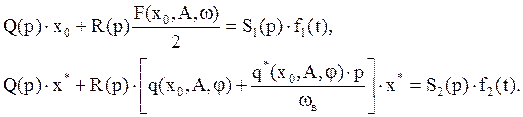
Так как решение ищем в виде x*=Asin(ωвt+φ), то решение x*=0 не удовлетворяет, поэтому далее рассматриваем уравнение
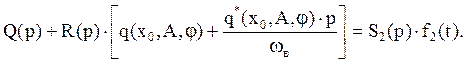 (2)
(2)
Делаем замену p=jωв и выражаем f2(t):
![]()
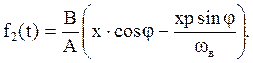
Тогда уравнение (2) будет:
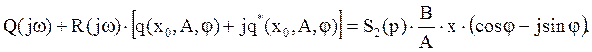 Правая часть этого выражения представляет
собой комплексное число в тригонометрической форме, преобразуем его в показательную,
в результате получаем уравнение (добавить самостоятельно):
Правая часть этого выражения представляет
собой комплексное число в тригонометрической форме, преобразуем его в показательную,
в результате получаем уравнение (добавить самостоятельно):
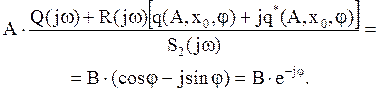
Это уравнение можно решить графически и аналитически, но в любом случае имеем два уравнения (вещественной и мнимой частей) и три неизвестных (А, х0 и φ). В результате решения получаем:
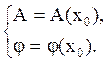 (3)
(3)
После нахождения А и φ подставляем их в функцию F(A(x0),φ(x0)) и получаем функцию смещения, которая может быть линеаризована обычным способом: Ф(х0)=кх0.
Функцию смещения подставляем в уравнение (1) и из этого уравнения находим х0(t) через обратное преобразование Лапласа (добавить самостоятельно), найденную функцию х0(t) подставляем в систему (3) и находим А и φ.
Если функция смещения Ф(х0) не допускает линеаризации в обычном смысле (получается в виде нелинейного элемента), то производят повторную линеаризацию с функцией Ф(х0). Далее процедура нахождения колебаний повторяется.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.