Методы случайного поиска. Адаптивный метод случайного поиска. Метод случайного поиска с возвратом при неудачном шаге

Методы случайного поиска

Постановка задачи

Пусть дана функция f(x), ограниченная снизу на множестве Rⁿ и имеющая непрерывные частные производные во всех его точках.

Требуется найти безусловный минимум функции f(x) многих переменных, т.е. найти такую точку x^*ÎRⁿ, что

Основная идея заключается в том, чтобы перебором случайных значений независимых переменных найти оптимум целевой функции или направление движения к нему. Общим для всех методов является применение случайных чисел в процессе поиска.

Адаптивный метод случайного поиска

Стратегия поиска

Задается начальная точка x⁰. Каждая последующая точка находится по

гдеt_k > 0 – величина шага; x^k – случайный вектор единичной длины (определяется в n-мерном пространстве и предполагается что он с равной степенью вероятности может принимать любое направление в этом пространстве), определяющий направление поиска; k– номер итерации. На текущей итерации при помощи генерирования случайных векторов x^k получаются точки, лежащие на гиперсфере радиуса t_k с центром в точке x^k (рисунок 1). Если значение функции в полученной точке не меньше, чем в центре, шаг считается неудачным (точки y¹, y² при поиске из x⁰; y¹, y³ при поиске из x¹). Если число неудачных шагов из текущей точки достигает некоторого числа М, дальнейший поиск продолжается из той же точки, но с меньшим шагом до тех пор, пока он не станет меньше заранее заданной величины R. Если же значение функции в полученной точке меньше, чем в центре, шаг считается

Алгоритм

Шаг 1. Задаем начальную точку x⁰, коэффициенты расширения a≥1 и 0<b<1, M – максимальное число неудачно выполненных испытаний на текущей итерации, t₀ = 1 – начальную величину шага, R – минимальную величину шага, N – максимальное число итераций. Полагаем k=0, j=1.

Шаг 2. Получаем случайный вектор  где x_i^j – случайная величина, равномерно распределенная на интервале [–1, 1].

Шаг 3. Вычисляем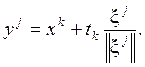

Шаг 4. Проверяем выполнение условий

а) если f(y^j) < f(x^k), шаг удачный. Полагаем z^j = x^k + a(y^j – x^k). Определяем, является ли текущее направление y^j – x^k удачным:

-  если f(z^j) < f(x^k), направление поиска удачное. Полагаем x^k+1 = z^j, t_k+1 = at_k, k=k+1 и проверяем условие окончания. Если k<N, полагаем j=1 и переходим к шагу 2. Если k=N, поиск завершаем: x^* @ x^k;

-  если f(z^j) ≥ f(x^k), направление поиска неудачное, переходим к шагу 5;

б) если f(y^j) ≥ f(x^k), шаг неудачный и переходим к шагу 5.

Шаг 5. Оцениваем число неудачных шагов из текущей точки:

а) если j<М, полагаем j= j + 1 и переходим к шагу 2;

б) если j=М, проверяем условие окончания:

-  если t_k≤ R, процесс заканчивается: x^* @ x^k, f(x^*) @ f(x^k);

-  если t_k> R, полагаем t_k= bt_k, j=1 и переходим к шагу 2.

Замечания:

1. Величина x_i^j, равномерно распределенная на интервале [–1, 1], генерируется обычно с помощью датчиков псевдослучайных чисел на ЭВМ. Вырабатывается случайная величина h_i^j, равномерно распределенная на интервале [0, 1], а затем используется линейное преобразование: x_i^j = 2h_i^j – 1.

2. Рекомендуются следующие параметры алгоритма: a = 1,618; b = 0,618; М = 3n. Начальный шаг t₀≥R можно задать произвольно.

3. Если выполнено условие окончания t_k≤ R, то в качестве ответа можно использовать любую точку внутри шара с радиусом t_k и центром в точке x^k.

Метод случайного поиска с возвратом при неудачном шаге

Стратегия поиска

Задается начальная точка x⁰. Каждая последующая точка находится по

гдеt_k > 0 – величина шага; x^k – случайный вектор единичной длины, определяющий направление поиска; k– номер итерации. На текущей итерации при помощи генерирования случайных векторов x^k получаются точки, лежащие на гиперсфере радиуса t_k с центром в точке x^k (рисунок 2). Если значение функции в полученной точке не меньше, чем в центре, шаг считается неудачным (точки y¹, y² при поиске

Шаг 1. Задаем начальную точку x⁰, коэффициент сжатия 0<b<1, M – максимальное число неудачно выполненных испытаний на текущей итерации, t₀ = 1 – начальную величину шага, R – минимальную величину шага, N – максимальное число итераций. Полагаем k=0, j=1.

Шаг 2. Получаем случайный вектор  где x_i^j – случайная величина, равномерно распределенная на интервале [–1, 1].

Шаг 3. Вычисляем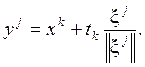

Шаг 4. Проверяем выполнение условий

а) если f(y^j) < f(x^k), шаг удачный. Полагаем x^k+1 = y^j, t_k+1 = t_k, k=k+1 и проверяем условие окончания. Если k<N, полагаем j=1 и переходим к шагу 2. Если k=N, поиск завершаем: x^* @ x^k;

б) если f(y^j) ≥ f(x^k), шаг неудачный и переходим к шагу 5.

Шаг 5. Оцениваем число неудачных шагов из текущей точки:

а) если j<М, полагаем j= j + 1 и переходим к шагу 2;

б) если j=М, проверяем условие окончания:

-  если t_k≤ R, процесс заканчивается: x^* @ x^k, f(x^*) @ f(x^k);

-  если t_k> R, полагаем t_k= bt_k, j=1 и переходим к шагу 2.

Метод наилучшей пробы

Стратегия поиска

Задается начальная точка x⁰. Каждая последующая точка находится по

гдеt_k > 0 – величина шага; x^k – случайный вектор единичной длины, определяющий направление поиска; k– номер итерации. На текущей итерации при помощи генерирования случайных векторов x^k получаются М точек y¹, …, y^М, лежащих на гиперсфере радиуса t_k с центром в точке x^k (рисунок