Методы одномерной безусловной оптимизации (для интервала поиска 1<х<3 при точности ε=0,04)

Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт цветных металлов и материаловедения

Кафедра автоматизации производственных процессов

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

Методы одномерной безусловной оптимизации

Вариант 18

Преподаватель                                                                              Г.Б. Даныкина

Студент      МФ 07-09                                                                   М.С. Карпухина

Красноярск 2011

Цель работы: ознакомиться с методами решения задач одномерной безусловной оптимизации, а также научиться решать задачи расчетным и графическим способами.

Ход работы

Решим задачу одномерной оптимизации методом дихотомии для интервала поиска 1<х<3 при точности ε=0,04 для функции l:

G(x)=3(x-2,5)²+2

Ход решения методом дихотомии представлен на рисунке 1.

Рисунок 1 – Ход графического решения методом дихотомии

На отрезке [a₀,b₀] выберем два значения по формулам:

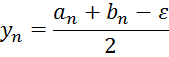
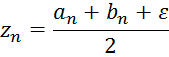
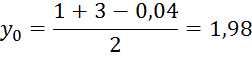
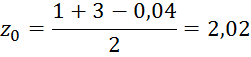
Найдем значений функции в этих точках.

f(y₀)=3(1,98=2,5)²+2=2,8112,

f(z₀)=3(2,02-2,5)²+2=2,6912.

Поскольку f(y₀)>f(z₀), берем y₀=a₁, b₀=b₁.

Гарантированный интервал неопределенности находим по формуле:

L₁=(b₀+a₀+ ε)/2,

L₁=(3+1+0,04)/2=1,02.

На отрезке [a₁,b₁] выбираем два значения y₁ и z₁.

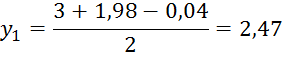
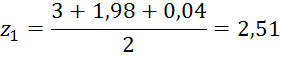
Вычислим значение функции в данных точках.

f(y₁)=3(2,47-2,5)²+2=2,0027,

f(z₁)=3(2,51-2,5)²+2=2,0003.

Так как f(y₁)>f(z₁), берем y₁=a₂, b₁=b₂.

При этом гарантированный интервал неопределенности определяем по формуле:

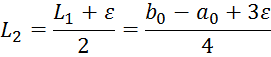
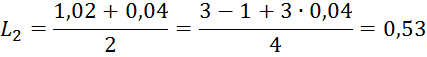
На интервале [a₂,b₂] выберем два значения y₂, z₂:

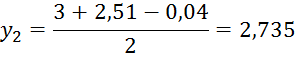
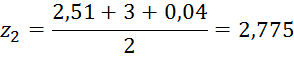
Найдем значение функции в этих точках.

f(y₂)=3(2,735-2,5)²+2=2,17,

f(z₂)=3(2,775-2,5)²+2=2,23.

Так как f(y₂)<f(z₂) берем a₂=a₃, z₂=b₃.

Вычислим

И проверим условие окончания

L₃=b₃-a₃=2,775-2,47=0,305.

Процесс поиска завершается, поскольку L₃<ε.

Локальный экстремум находится на интервале [a₃,b₃]. В качестве приближенного решения возьмем середину последнего интервала

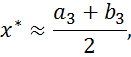
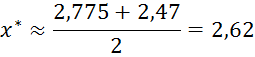
Сходимость найдем по формуле:

.

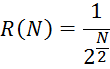
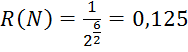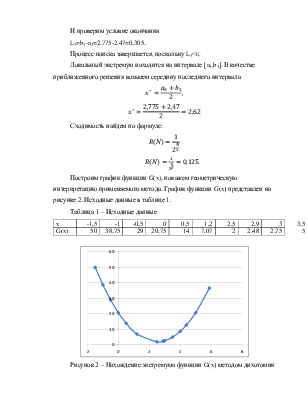
Построим график функции G(x), покажем геометрическую интерпретацию применяемого метода. График функции G(x) представлен на рисунке 2. Исходные данные в таблице 1.

Таблица 1 – Исходные данные

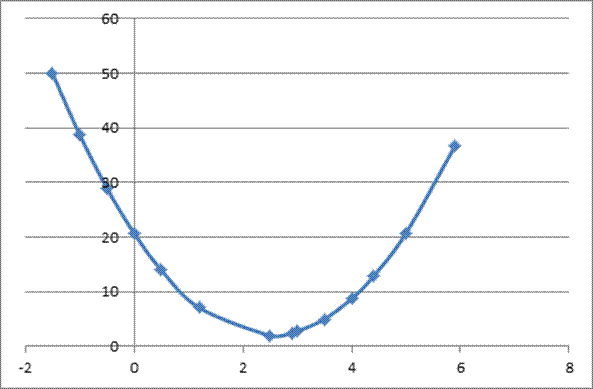
Рисунок 2 – Нахождение экстремума функции G(x) методом дихотомии