Методы нелинейного программирования. Безградиентные методы. Метод дихотомии. Метод золотого сечения

Требуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку x^*ÎR, что .

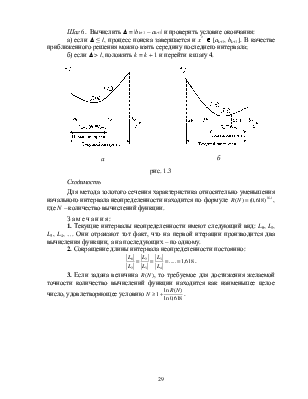
Большинство известных методов одномерной минимизации применяется для класса унимодальных функций. Функция f(x) называется унимодальной на интервале L₀=[a₀, b₀], если она достигает локального экстремума на нем в единственной точке x^*, причем слева от x^* эта функция строго убывает, а справа – строго возрастает. Если a₀ ≤ y < z < x^*, то f(y) > f(z), а если x^* < y < z ≤ b₀, то f(y) < f(z).

Отрезок L₀, которому принадлежит x^*, назовем отрезком локализации минимума, или интервалом неопределенности (в литературе).

Если целевая функция унимодальная, то можно сузить интервал неопределенности путем определения значений целевой функции в двух точках интервала задания функции f(y) и f(z) и последующего поинтервального сравнения. Последовательно сужая интервал исследования, на котором находится оптимальное значение искомой переменной, можно с достаточной степенью точности найти оптимальное значение целевой функции.

Стратегии поиска

Существует две стратегии выбора точек, в которых производится вычисление значений функций. Если все точки задаются заранее, до начала вычислений, – это пассивная (параллельная) стратегия. Если эти точки выбираются последовательно в процессе поиска с учетом результата предыдущих вычислений, – это последовательная стратегия.

Стратегия включает в себя следующие этапы:

1.  Выбор начального интервала неопределенности. Границы a₀, b₀ интервала должны быть такими, чтобы функция f(x) была унимодальной.

2.  Уменьшение интервала неопределенности (в качестве нового интервала берется «гарантирующий интервал», наверняка содержащий точку минимума).

3.  Проверку условия окончания. Поиск заканчивается, когда длина текущего интервала неопределенности [a_k, b_k] оказывается меньше установленной величины.

Ответом является множество точек, принадлежащих последнему интервалу неопределенности, среди которых каким-либо образом выбирается решение задачи x^*. Обычно это середина интервала [a_k, b_k].

К последовательным стратегиям поиска экстремума унимодальных функций относятся методы дихотомии, золотого сечения и Фибоначчи.

Метод дихотомии

Стратегия поиска

Задается начальный интервал неопределенности и требуемая точность. Алгоритм опирается на анализ значений функции в двух точках. Для их нахождения текущий интервал неопределенности делится пополам и в обе стороны от середины откладывается по , где e – малое положительное число. Условия окончания процесса поиска стандартные: поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.

Алгоритм

Шаг 1.  Задать начальный интервал неопределенности L₀=[a₀, b₀],
e > 0 – малое число, l > 0 – точность.

Шаг 2.  Положить k = 0.

Шаг 3.  Вычислить

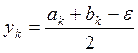; f(y_k),  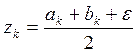      , f(z_k).

Шаг 4.  Сравнить f(y_k) и f(z_k):

а) если f(y_k)  f(z_k), положить a_k+1 = a_k, b_k+1 = z_k и перейти к шагу 5;

б) если f(y_k) > f(z_k), положить a_k+1 = y_k, b_k+1 = b_k.

Шаг 5.  Вычислить |L_2(k+1)| = |b_k+1 – a_k+1| и проверить условие окончания:

а) если |L_2(k+1)| ≤ l, процесс поиска завершается и x^* Î L_2(k+1) = [a_k+1, b_k+1]. В качестве приближенного решения можно взять середину последнего интервала:
;

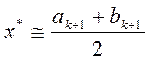б) если |L_2(k+1)| > l, положить k = k + 1 и перейти к шагу 3.

(Примечание: текущие интервалы неопределенности L₀, L₂, L₄ имеют