Исследование устойчивости систем автоматического регулирования по критерию Гурвица и синтез систем методом логарифмических частотных характеристик, страница 9

Рассматривая разомкнутую передаточную функцию исходной системы, постараемся выделить в ней известные нам типовые звенья. АСР состоит из:  исполнительного двигателя, тахогенератора, двигателя и электромашинного усилителя. Таким образом, если рассматривать систему с точки зрения типовых звеньев, то мы видим, что система представлена:

· Интегрирующим звеном (исполнительный двигатель) с передаточной функцией .

· Пропорциональным звеном, реализуемым тахогенератором, с передаточной функцией

· Колебательным звеном, которое реализует двигатель, с передаточной функцией .

· Двумя инерционными звеньями первого порядка (электромашинный усилитель) с передаточными функциями соответственно

 и  .

Так как все элементы соединены последовательно, то чтобы получить разомкнутую систему передаточные функции их перемножаются, а чтобы получить ЛАЧХ этой системы в этом случаем мы сложим соответствующие характеристики всех элементов АСР. Таким образом, получим выражение для ЛАЧХ некорректированной системы, которое будет иметь вид:

 .

 Построив соответствующие характеристики и сложив их алгебраически на плоскости, получим ЛАЧХ некорректированной системы.

2.1.1 ПОСТРОИМ ЛАЧХ ИСПОЛНИТЕЛЬНОГО ДВИГАТЕЛЯ

Как уже было сказано выше исполнительный двигатель это интегрирующее звено с соответствующей передаточной функцией

,

и конкретно в нашем случае

.

ЛАЧХ интегрирующего звена представляет собой прямую, с наклоном

–20дб/дек, проходящую через точку ω=K, а на частоте ω=1 амплитуда будет равна 20lgK=20lg18,32=25,25 дб.

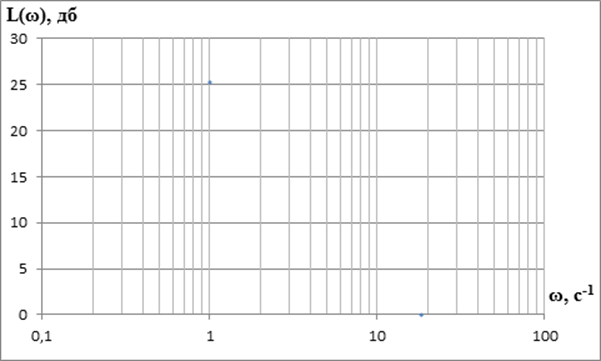
Рисунок 6–ЛАЧХ интегрирующего звена

2.1.2 ПОСТРОИМ ЛАЧХ ПРОПОРЦИОНАЛЬНОГО ТАХОГЕНЕРАТОРА

Передаточная функция пропорционального звена (тахогенератора) в нашем случае будет иметь вид:

.

ЛАЧХ пропорционального звена представляет собой прямую параллельную оси абсцисс и отстоящую от ней на величину 20lgK. В данном случае эта величина будет равна 20lgK=20lg0,004=–48 дб.

Рисунок 7–ЛАЧХ пропорционального звена

2.1.3 ПОСТРОЕНИЕ ЛАЧХ ДИГАТЕЛЯ

Передаточная функция двигателя имеет вид:

Для колебательного звена можно построить как точную так и приближенную (асимптотическую) ЛАЧХ, в данном случае мы будем строить приближенную ЛАЧХ которая состоит из двух участков: первого от 0 до ω₀(на которой она представляет собой прямую параллельную оси абсцисс и отстоящую от неё на величину 20lgK) и второго от ω₀ до ∞ (на этом участке ЛАЧХ представляет собой прямую с наклоном –40 дб/дек). Её можно построить если выполняется условие: коэффициент затухания

,

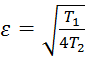а в конкретном случае для двигателя

,

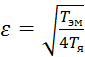должен находиться в диапазоне 0,35 ≤ ε ≤ 0,7.

Найдем коэффициент затухания:

,

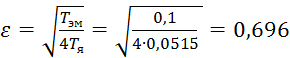данный коэффициент затухания попадает в нужный нам диапазон изменения, поэтому мы можем спокойно строить асимптотическую ЛАЧХ колебательного звена.

Рассчитаем параметры для построения асимптотической ЛАЧХ колебательного звена, а именно ω₀ и величину 20lgK:

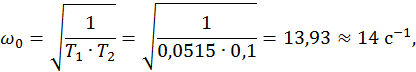
Таким образом ЛАЧХ колебательного звена будет иметь вид:

Рисунок 8–ЛАЧХ колебательного звена

2.1.4 ПОСТРОЕНИЕ ЛАЧХ ЭЛЕКТРОМАШИННОГО УСИЛИТЕЛЯ

Рассмотри передаточные функции двух инерционных звеньев первого порядка, в нашем случае они будут иметь вид представленный ниже:

,   .

ЛАЧХ инерционного (апериодического звена) также будем строить приближенную, как и асимптотическая ЛАЧХ колебательного звена, данная характеристика состоит из двух участков отличие лишь в том, что наклон прямой на втором участке будет равен –20 дб/дек, также рассчитаем параметры, а конкретно для обоих случаев величину 20lgK и частоту сопряжения двух ω:

первый случай ,

второй случай  ,

Таким образом ЛАЧХи этих звеньев будут выглядеть следующим образом:

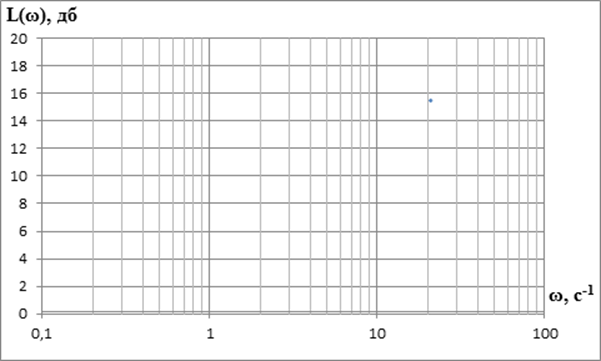
Рисунок 9–ЛАЧХ первого инерционного звена первого порядка

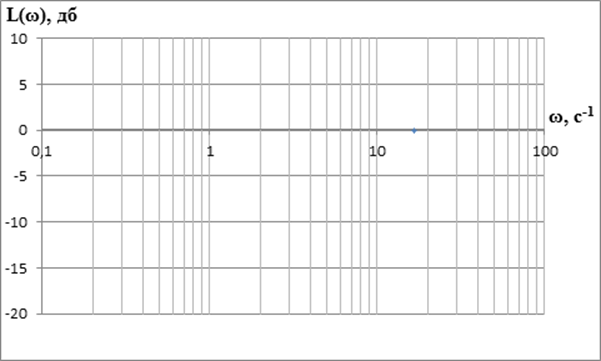
Рисунок 9–ЛАЧХ второго инерционного звена первого порядка

2.1.5 ПОСТРОЕНИЕ ЛАЧХ НЕКОРРЕКТИРОВАННОЙ СИСТЕМЫ

Для того чтобы построить ЛАЧХ некорректированной системы как уже и было сказано ранее нужно сложить всех характеристики элементов АСР на плоскости это видно из выражения:

 .

Выполним суммирование логарифмических амплитудных частотных характеристик на плоскости (рисунок 10).

2.2  ПОСТРОЕНИЕ ЛАЧХ ЖЕЛАЕМОЙ СИСТЕМЫ