Исследование устойчивости систем автоматического регулирования по критерию Гурвица и синтез систем методом логарифмических частотных характеристик, страница 3

Наша АСР устойчивая, найдем критический коэффициент усиления, для этого сначала запишем передаточную функцию с учетом найденного коэффициента системы:

Далее в определитель Гурвица, вместо К_с подставим в нашем случае К_кр (поскольку система астатическая) и как уже и действовали ранее для нахождения К_ид, находим К_кр:

Как и в предыдущем случае получаем два корня из характеристического уравнения, и опять действуя с точки зрения физического смысла, учитываем только положительный корень, а именно наш искомый критический коэффициент усиления нашей АСР будет равен K_кр=8,1856.

1.5 РАСЧЕТ ВЕЩЕСТВЕННОЙ ЧАСТОТНОЙ ХАРАКТЕРИСТИКИ ЗАДАННОЙ СИСТЕМЫ И ПОСТРОЕНИЕ ПЕРЕХОДНОГО ПРОЦЕССА ПО ЗАДАЮЩЕМУ ВОЗДЕЙСТВИЮ ПРИБЛИЖЕННЫМ МЕТОДОМ ТРАПЕЦИЙ

Зная передаточную функцию системы, с помощью ПП MathCad, путем подстановки p=jω, получаем комплексную передаточную функцию, далее задаваясь значениями 0≤ω<∞, строим вещественную частотную характеристику (ВЧХ) (рисунок 3).

Следующим этапом после построения ВЧХ, разбиваем её на трапеции, с учетом правил разбивки:

1. Строим касательные ко всем точкам перегиба.

2. Строим касательные к наклонным участкам ВЧХ.

3. Количество трапеций должно быть минимальным, но их площадь должна максимально повторять площадь ограниченную ВЧХ.

4. Все трапеции одной стороной должны прилегать к оси ординат. Трапеции могут быть перевернутыми.

5. Сумма высот всех трапеций должна быть равна значению ВЧХ при ω=0.

После разбивки ВЧХ на трапеции составляем уравнение ВЧХ, в нашем случае оно будет иметь вид:

P_з(ω)=–Тр1–Тр2+Тр3–Тр4–Тр5–Тр6

Проверим выполнения пятого правила:

 P_з(0).

После разбивки, определяем параметры каждой трапеции, данные заносим в таблицу 4.

Таблица 4–Параметры трапеций

Далее для каждой трапеции заполняем таблицу истинных значений времени t и переходной функции h(t). Для этого из справочника выписываем значения τ и h(τ), для полученной выше величины æ. Переход от табличных значений к истинным выполняем по формулам (таблицы 5, 6, 7, 8, 9, 10):

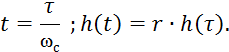
Таблица 5–Значение h(t) – функции для трапеции 1

Продолжение таблицы 5

Продолжение таблицы 5