Изучение программы настройки, анализа, синтеза и имитационного моделирования промышленных САР “IPC-CAD” в режиме “Одноконтурные САР”, страница 3

Передаточная функция И-регулятора описывается выражением

W(s) = Y(s)/X(s) = 1/(T_и s) = К_и/s.

Пропорционально–интегральный закон регулирования

Пропорционально–интегральный закон выражается уравнением

                                                .

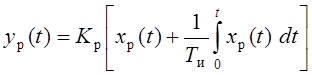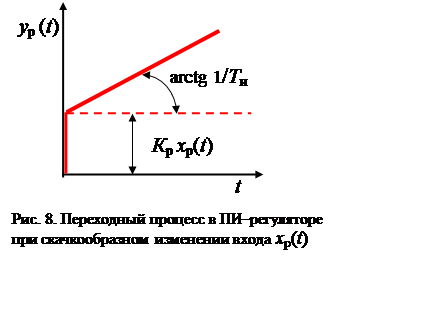
Выходной сигнал ПИ-регулятора состоит из суммы двух составляющих – пропорциональной и интегральной  (рис.8).

Передаточная функция ПИ-регулятора описывается выражением

.

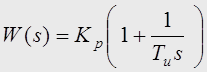Данные регуляторы обладают ценным свойством отсутствия статической ошибки регулируемой величины при их использовании в САР.

Пропорционально–интегрально–дифференциальный закон регулирования

ПИД-закон регулирования определяется уравнением

 ,

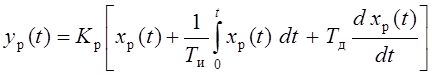где  Т_д  - время дифференцирования (предварения).

Параметрами настройки этих регуляторов являются: коэффициент пропорциональности  K_p   и постоянные времени T_и  и  T_д . 

Передаточная функция ПИД-регулятора описывается выражением

.

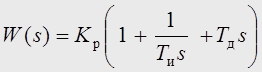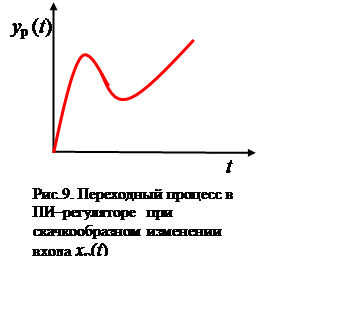
При скачкообразном изменении регулируемой величины (х_р), реальный ПИД- регулятор оказывает мгновенное воздействие на регулирующий орган за счет действия дифференциальной составляющей (рис. 9), затем величина воздействия падает до значения, определяемого пропорциональной частью регулятора, после чего постепенно начинает оказывать свое влияние интегральная часть регулятора.

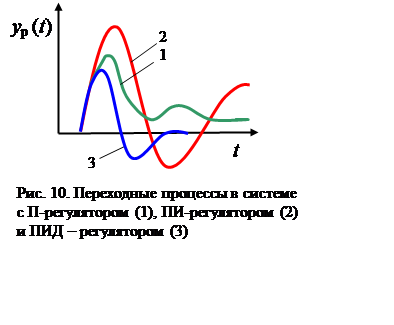
Переходные процессы в системе при регулировании П-регулятором, ПИ-регулятором и ПИД-регулятором (рис. 10) показывают преимущество ПИД-регулятора, которое состоит в том, что процесс протекает с меньшей динамической ошибкой и заканчивается значительно быстрее.

ПИД-закон регулирования особенно целесообразно применять на объектах с резкими и значительными возмущениями. 

Понятие об устойчивости САР

Устойчивость, как и качество регулирования, является одним из основных требований, предъявляемых к САР.

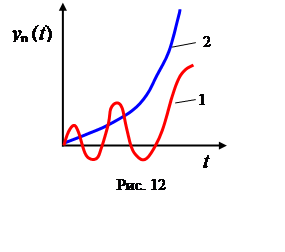
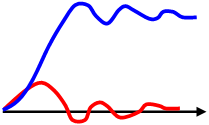
САР является устойчивой, если при каком-то случайном воздействии на нее она приводит регулируемый параметр к новому или к первоначальному устойчивому равновесию. Переходные процессы в устойчивой и неустойчивой САР при возмущении (кривые 1) и при изменении задания (кривые 2) приведены на рис. 11 и 12. Неустойчивая САР не пригодна к использованию.

								t
			Рис. 11

Качество регулирования в САР

Одним из основных требований, предъявляемых к САР, является ее устойчивость, которую определяют с помощью различных критериев устойчивости (Найквиста, Михайлова и др.) либо путем решения дифференциального уравнения, описывающего данную систему. Однако устойчивость САР является необходимым, но не достаточным условием технической пригодности системы. Для работоспособности системы не менее необходимо, чтобы процесс автоматического регулирования осуществлялся при обеспечении определенных качественных показателей.

Качество процесса регулирования системы, как правило, оценивают по графику переходного процесса (рис. 13), который получают путем решения дифференциального уравнения системы на ЭВМ или используя приближенные методы (по вещественной частотной характеристике замкнутой системы и т.д.).

Основными показателями качества регулирования являются: максимальное динамическое отклонение регулируемой величины y₁, перерегулирование h, статическая ошибка y_сти время регулирования t_р. Эти показатели зависят, в основном, от свойств объекта и регулятора.

Максимальным динамическим отклонением регулируемой величины у₁ называется максимальная амплитуда отклонения регулируемой величины от своего номинального (заданного или исходного y_исх ) значения (рис. 13).

Временем регулирования t_p  называется время, за которое регулируемая величина приводится к (старому) новому установившемуся состоянию.

Перерегулированием h называют отношение

.

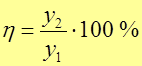Оно характеризует колебательность процесса. При  h = 0 переходной процесс апериодический (неколебательный).