Изучение программы настройки, анализа, синтеза и имитационного моделирования промышленных САР “IPC-CAD” в режиме “Одноконтурные САР”, страница 2

hоg(t) = hg(t)/Ag ..

(5)

          Если разброс между функциями h^о_g(t) незначителен (менее 3%), то для  последующей обработки выбирается любая из полученных переходных функций. В противном случае производится усреднение h^о_g(t) по множеству номеров g, то есть находят усредненную единичную переходную  функцию:

(6)

В некоторых случаях математическое описание объекта управления осуществляют по нормированной переходной функции h^н (t)

,

или

где h^о_g(T_у), (T_у) - значения единичной и усредненной единичной переходных функций при времени установления (T_у), соответственно.

          По переходным  функциям определяют величины: коэффициент усиления объекта (K_об), постоянные времени объекта (T), запаздывание (t).

          Коэффициент усиления объекта:

K_об = h^о_g(T_у)  или K_об =  (T_у).

          Величину запаздывания t  находят как отрезок времени, внутри которого выполняется неравенство 0 < h^о_g(t) < D ,  где величина  D  обычно составляет

(0,01¸0,02)  (T_у).

При математическом описании объектов управления в начале находят наиболее простую математическую модель объекта - линейное дифференциальное уравнение первого порядка с запаздывающим аргументом (после­довательного соединения апериодического звена и звена запаздывания). Последующий выбор регулятора и определение его приближенных настроек по формулам или номограммам основан на предположении, что объект аппроксимирован последовательным соединением  апериодического  звена и звена запаздывания.

После вычисления точности такой аппроксимации, в случае, если, она не удовлетворяет исследователя, порядок аппроксимирующего уравнения увеличивается. Причем повышение степени аппроксимирующего уравнения свыше двух нерационально, т.е. переходные характеристики объекта обычно определяются с точностью порядка 10-15%.

Вычисление аппроксимирующей (теоретической) переходной характеристики для ее анализа и сравнения с экспериментальной осуществляют по зависимостям:

-  для устойчивого объекта 1-го порядка

,

(5)

-  для устойчивого объекта  2-го порядка

,

(6)

Для оценки точности аппроксимации определяют среднеквадратичную погрешность

(6)

где  y_э (t), y_ап (t)  – значение экспериментальной и аппроксимирующей переходной функции в момент времени  t  соответственно;  yэ (Tу ) - установившееся значение экспериментальной переходной функции;  К - число точек  y_э (t)  и  y_ап (t).

Аппроксимация удовлетворительна, если погрешность  δ  не более 3%.

Регуляторы

Функционирование регуляторов происходит в соответствии с алгоритмом регулирования, описывающим зависимость  выходной величины регулятора от входной величины. Существуют несколько типовых алгоритмов (законов) регулирования:

-  пропорциональный (П-закон);

-  интегральный (И-закон);

-  пропорционально–интегральный (ПИ-закон);

-  пропорционально–интегрально–дифференциальный (ПИД-закон);

-    пропорционально–дифференциальный (ПД-закон);

-  двухпозиционный;

-  трехпозиционный.

Пропорциональный закон регулирования

Пропорциональный закон описывается уравнением

y_p (t) = К_p x_p(t) ,

где  y_p(t) _, x_p(t) – выходной и входной сигналы регулятора, К_p – коэффициент пропорциональности, являющийся параметром настройки П-регулятора.

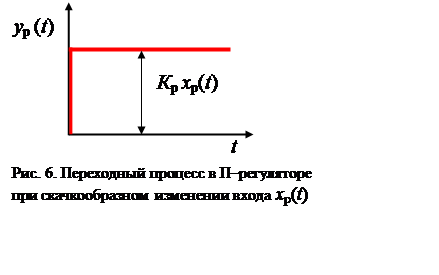У этих регуляторов отклонение регулируемой величины х от ее заданного значения х₀ вызывает  перемещение регулирующего органа на величину, пропорциональную этому отклонению (рис.6).

x_p= х  – х₀.

Передаточная функция П-регулятора равна   

W(s) = Y(s)/X(s) = К_p.

Интегральный закон регулирования

 Процесс регулирования происходит по закону, описываемому уравнением

,

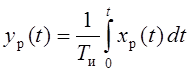где T_и – постоянная времени интегрирования – параметр настройки И-регулятора.

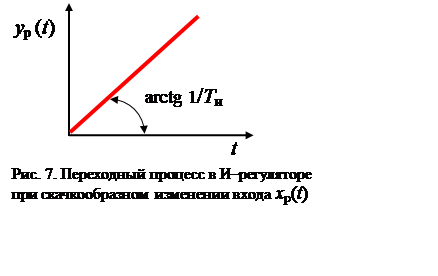 Интегральные регуляторы производят перемещение регулирующего органа, пропорционально интегралу изменения регулируемой величины до тех пор, пока не восстановится ее заданное значение (рис. 7) .