Изучение программы настройки, анализа, синтеза и имитационного моделирования промышленных САР “IPC-CAD” в режиме “Одноконтурные САР”

Красноярская государственная академия цветных металлов и золота

Кафедра автоматизации производственных процессов

ЦМ	Дисциплина “Системы Автоматизации” Красноярск  2002 г.

Лабораторная работа № 1

“Изучение программы настройки, анализа, синтеза

 и имитационного моделирования промышленных САР “IPC-CAD”

в режиме“Одноконтурные САР”

ЦЕЛЬ РАБОТЫ

1. Изучить состав и назначение программного продукта “IPC-CAD”.

2. Освоить расчет, настройку, анализ и синтез одноконтурной САР с помощью программы “IPC-CAD”.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Одноконтурные САР

Структура одноконтурных САР

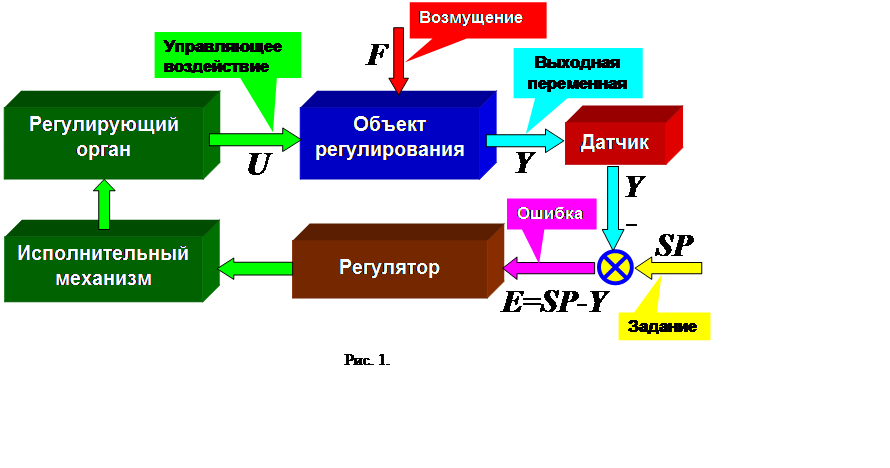
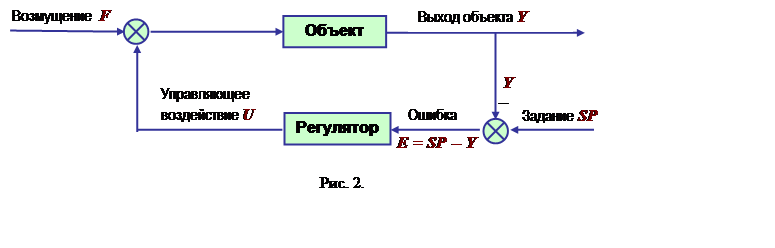
Одноконтурные системы автоматического регулирования (САР) являются основными составляющими нижнего (локального) уровня  автоматизированных систем управления технологическими процессами (АСУ ТП). Структурная схема одноконтурной САР приведена на рис. 1.

 

Отнеся исполнительный механизм (ИМ) и регулирующий орган (РО) к регулятору, эту схему можно представить в упрощенном виде (рис. 2).

 

Расчет САР заключается в выборе закона регулирования и определения настроечных параметров промышленных регуляторов, обеспечивающих оптимальный по устойчивости и по качеству процесс регулирования. Для расчета  необходимо знать статические (коэффициент усиления К_об)  и динамические (запаздывание  τ_об , постоянную времени Т_об) характеристики объекта регулирования.

Объекты регулирования

По реакции на возмущения объекты регулирования делятся на:

–  объекты с самовыравниванием;

–  объекты без самовыравнивания.

    К первым относятся устойчивые объекты,  ко вторым - нейтральные и неустойчивые.

Самовыравнивание - свойство объекта самостоятельно устанавливаться в равновесное состояние после изменения входной величины. Объекты с самовыравниванием  (устойчивые или статические)  можно представить апериодическими звеньями первого или второго порядков и их комбинациями.

Объекты без самовыравнивания (неустойчивые или астатические) в своей структуре содержат интегрирующие звенья. Примером нейтрального объекта может служить любая емкость или сосуд без стока, в которых уровень вещества или жидкости при открытии заслонки непрерывно растет 

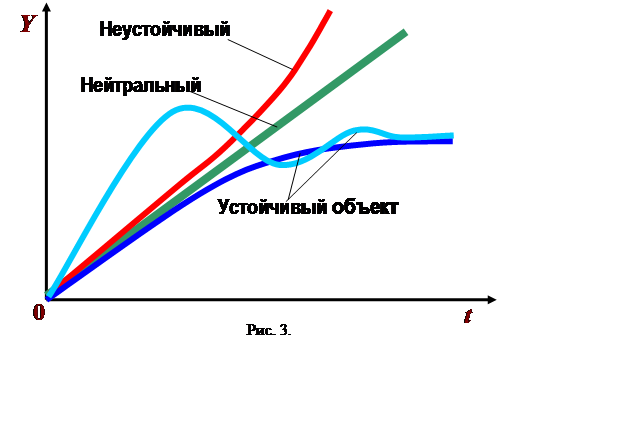
Переходные характеристики различных объектов, показывающие изменение выходной регулируемой величины Y  во времени  tпри подаче на них ступенчатого возмущения, приведены на рис. 3.

Передаточные функции объектов регулирования с запаздыванием имеют следующий вид:

– для статических объектов 

;

(1)

– для астатических объектов

,

(2)

где  ­ s - оператор Лапласа.

 

Обычно порядок nобъектов цветной металлургии равен 1, реже 2. Тогда для n= 1 передаточная функция статических объектов приобретает вид

.

(3)

У астатических объектов передаточная функция равна

.

(4)

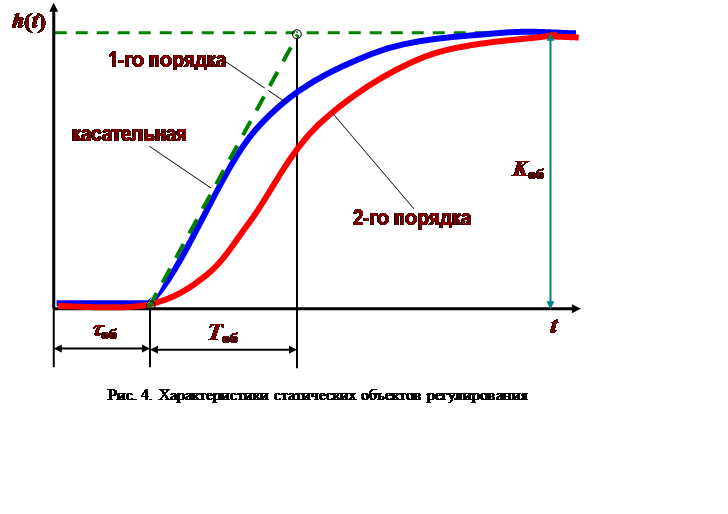
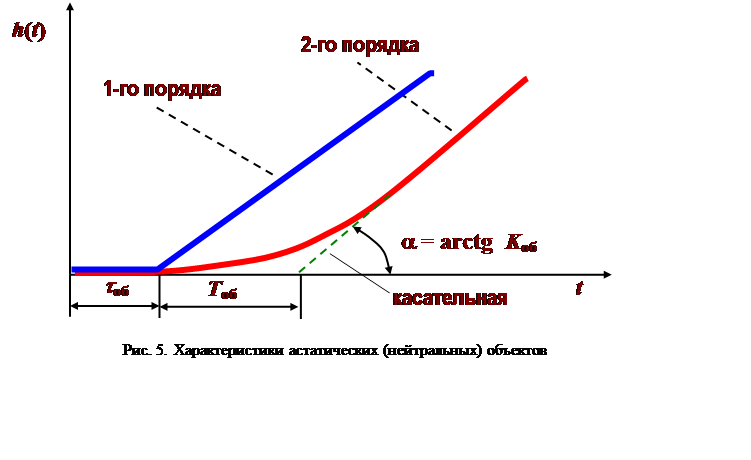
Переходные характеристики  h(t)  устойчивых и нейтральных объектов регулирования 1-го и 2-го порядков при подаче на них единичного ступенчатого воздействия  показаны на рис. 4 и 5.

Для определения статических и динамических характеристик объектов регулирования наиболее широко используются  активные экспериментальные методы, когда на вход объекта подают искусственные возмущения:

   1) апериодические ступенчатого или импульсного типа;

   2) периодические, гармонического характера.

Впервомслучае получают временные характеристики – кривые разгона и импульсные кривые разгона, во втором – частотные характеристики: амплитудно-фазовую (АФХ), амплитудно-частотную (АЧХ), фазово-частотную (ФЧХ).

 

Активные методы позволяют быстро получить информацию о статических и динамических свойствах объекта. Однако могут нарушить нормальный ход технологического процесса из-за значительного отклонения исследуемых величин.

 

Возмущения на входе объекта создают регулирующим органом, перемещаемым вручную или дистанционно. Величину возмущения – перемещение регулирующего органа выбирают исходя из условий работы исследуемого объекта.

Большие возмущения ведут к росту влияния нелинейностей и искажению результатов опытов, нарушению технологического процесса. Малые возмущения затрудняют регистрацию выходной величины на фоне случайных переходных процессов из-за неконтролируемых возмущений. По данным опытов, величина возмущения должна составлять 5-15 % от номинального значения входной величины при снятии кривой разгона и 15-25 % – при снятии  импульсной кривой разгона.

Обычно при проведении эксперимента снимается несколько переходных функций. Переходные функции h_g(t) при g = 1, 2, .., q, неискаженные помехами, строят в одном масштабе на графике. Так как при проведении эксперимента амплитуды A_g  входного сигнала были различны, то следует определить единичные переходные функции h^о_g(t) по формуле: