Задачи динамической оптимизации: Методические указания по проведению практических занятий и самостоятельной подготовки, страница 5

Необходимые и достаточные условия записываются в виде дифференциального уравнения Беллмана

,

(42)

с краевым условием . Если выражение в фигурных скобках непрерывно, и на него не наложено никаких ограничений (это соответствует классической постановке задачи динамической оптимизации), то из необходимого условия оптимальности

,

(43)

получаем выражение для экстремального (а в случае его единственности – оптимального) управления

.

(44)

Но пока мы не можем указать явное выражение для экстремального управления, поскольку уравнение Беллмана (42) еще не решено и потенциал S(X, t) не найден. Однако, если найденное управление, минимизирующее правую часть уравнения (42), подставить в него, то получим уравнение Гамильтона-Якоби относительно потенциала

,

(45)

с краевым условием , где

.

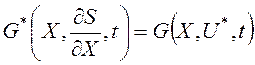Уравнения (44) и (45) позволяют найти оптимальное управление и потенциал (функцию Беллмана-Ляпунова). Решение уравнения (45) можно найти лишь  простейших случаях, поскольку в общем случае оно нелинейно. Удобно представить его в иной форме, как это было сделано в случае принципа максимума и вариационного исчисления выше.

Для этого определим гамильтониан

,

(46)

где вектор-функция  представляющая правую часть уравнений объекта, и тогда, вместо одного скалярного уравнения в частных производных (45), перейдем к двум векторным (или 2n скалярным) обыкновенным дифференциальным уравнениям относительно состояния и градиента потенциала, обозначенного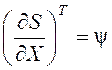

.

(47)

Индекс Т означает транспонирование.

Решим задачу – определение оптимального расхода дутья в конверторе, сформулированную в практическом занятии 3, методом динамического программирования.

Запишем необходимые и достаточные условия в виде дифференциального уравнения Беллмана (42), которое в нашем случае примет вид

.

(48)

Если считать, что ограничений на U не накладывается, то воспользуемся уравнением (43) и получим

.

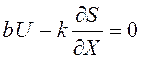Откуда оптимальное управление выразится как

.

(49)

Для получения выражения для X(t) и  воспользуемся системой уравнений (47) и получим

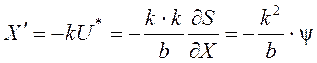, y¢ = 0, y = C.

Решая первое из этих равнений и учитывая, что y = C, получим

.

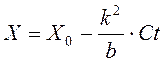Для того, чтобы определить величину С воспользуемся знанием величины  и получим, как и ранее,

.

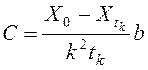Подставив эту величину в выражение (49), имеем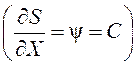

.

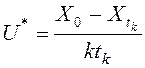Это выражение полностью совпадает с результатом, полученным принципом максимума. С учетом ограничений, наложенных на уравнение (49) окончательно получим

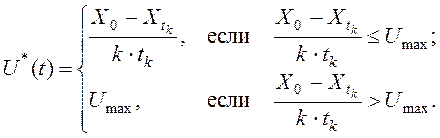
Это решение совпадает с решением, полученным с использованием принципа максимума.

Литература

1. Курс методов оптимизации / А.Г. Сухарев, А.В. Тимохов, В.В. Ведоров. – М: Наука, 1986. – 328 с.

2. Глинков Г.М., Климовицкий М.Д. Теоретические основы автоматического управления металлургическими процессами: учебное пособие для вузов. – М.: Металлургия, 1985. – 304 с.

3. Теория автоматического управления, ч. 2 / Под ред. А.В. Нетушила. – М: Высшая школа, 1972. – 432 с.

Оглавление

Практическое занятие 1 Краткая характеристика методов и формулировка задачи оптимального управления………………………………………………………
Практическое занятие 2 Уравнение Эйлера и его применение для решения задач оптимального управления………………………………………………………
Практическое занятие 3 Принцип максимума Понтрягина и его применение для решения задач оптимального управления………………………………………………………
Практическое занятие 4 Динамическое программирование. Уравнение Беллмана и его применение для решения задач оптимального управления……………..
Литература……………………………………………………………………….