Задачи динамической оптимизации: Методические указания по проведению практических занятий и самостоятельной подготовки, страница 4

в момент времени t = t_k выполняется соотношение y₀(t) ≤ 0 и , X(t) = 0 (после подстановки в выражение критерия оптимальности I управления U = U^*, функция I зависит от y и X).

Рассмотрим в качестве примера управление процессом конвертирования меди, целью которого является получение штейна заданного состава, за заданное время путем продувания расплава воздухом, обогащенным кислородом. Математическое описание процесса конвертирования в рабочем диапазоне изменения количества дутья представляют следующим линейным дифференциальным уравнением:

где  – расход дутья, являющийся управлением; Х – концентрация сульфидов железа в расплаве; k – коэффициент пропорциональности.

Требуется таким образом изменять управление U(t), чтобы обеспечить достижение заданного значения концентрации сульфидов в расплаве за определенное время протекания процесса t_k, т.е. X(t_k) =  и минимум критерия оптимальности

где b – коэффициент пропорциональности.

Критерий (38) выражает стремление достичь требуемую цель, экономя материальные затраты, связанные с дутьем. В соответствии с выражением (35) составим гамильтониан

На управление наложены ограничения типа (5) U – U_max ≤ 0, т.е.
0 ≤ U ≤ U_max.

Необходимые условия оптимальности на основании теоремы принципа максимума запишутся в виде

Из последнего уравнения системы (40) получим, что

.

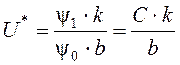Подставив выражение U^* в третье уравнение системы (40) и учитывая, что 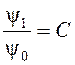, получим

.

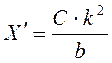Решая это уравнение, имеем следующее выражение оптимальной траектории

.

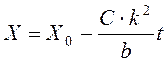Учитывая значение X = , вычислим величину

.

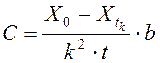Отсюда определяем 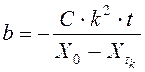, тогда

.

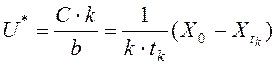Тогда оптимальное управление U^*(t) в соответствии с условием (5) можно записать как:

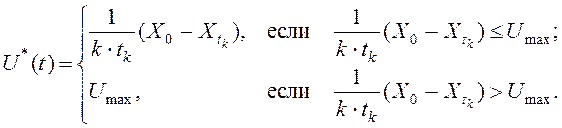
Таблица 2 – Варианты задач по применению принципа максимума Понтрягина и уравнения Беллмана

Практическое занятие 4

Динамическое программирование. Уравнение Беллмана и
его применение для решения задач оптимального управления

Классические методы нахождения экстремума функции многих переменных при большом числе переменных могут оказаться неприменимыми, и, поэтому, более целесообразно принимать решения о значениях функции U(t_i) не сразу (за один шаг), а постепенно, шаг за шагом. Такие процессы решения называют многошаговыми.

Математическим аппаратом изучения многошаговых оптимальных решений является динамическое программирование, созданное в значительной мере Р. Беллманом и его учениками в пятидесятых годах ХХ в.

Метод динамического программирования базируется на постулате, получившем название принципа оптимальности, и суть его заключается в следующем:

оптимальное поведение обладает тем свойством, что каковы бы ни были первоначальное состояние и решение в начальный момент, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.

Для получения необходимых и достаточных условий оптимальности водится скалярная функция S, называемая потенциалом или функцией Беллмана-Ляпунова; как минимальное значение критерия оптимальности, которое получается для заданного в какой-либо момент времени t состояния (X, t) при оптимальном управлении