Задачи динамической оптимизации: Методические указания по проведению практических занятий и самостоятельной подготовки, страница 2

Подставив выражение  в уравнения (7) и (8), получим однородную систему уравнений с соответствующими начальными и конечными условиями, решая которую находим оптимальные траектории движения системы  и .

Выразив  через  и , находим оптимальное программное управление . Если исключить время из ,  и , то можно найти  (оптимальное управление с обратной связью).

Однако следует иметь в виду, что наша задача является, так называемой, двухточечной краевой задачей, т.к. значения  задаются в моменты времени t₀ и t_k. Если аналитическое решение системы уравнений (7)-(9) встречает трудности (а на практике это повсеместно), то необходимо использовать численные методы решения дифференциальных уравнений. Для оценки итеративной процедуры выбора  целесообразно ввести некоторый функционал оценки близости, например:

Практическое занятие 2

Уравнение Эйлера и его применение для решения задач
оптимального управления

Для нахождения функции U(t), доставляющей экстремум функционалу

уравнение Эйлера имеет вид

где , .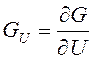

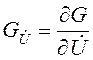В большинстве технических приложений вариационного исчисления функции, доставляющие экстремум функционалу, подчинены некоторым дополнительным условиям (уравнениям связи).

Для задач управления – это уравнения управляемого объекта вида

Для решения вариационных задач в этом случае используют метод неопределенных множителей Лагранжа, суть которого состоит в том, что уравнения Эйлера составляют для вспомогательной скалярной функции, называемой гамильтонианом:

где  – множители Лагранжа.

Функция U(t) и множители , …,  находят из системы (n+1) уравнений: уравнение Эйлера для функции (14) и n уравнений (13) математической модели объекта. Сформулированную задачу на условный экстремум называют общей задачей Лагранжа.

Рассмотрим пример применения уравнений Эйлера для решения задач оптимального управления.

Пример: управление двигателем постоянного тока. Допустим, что имеется возможность управления током якоря двигателя постоянного тока с независимым возбуждением (рис. 1). Примем, что магнитный поток Ф неизменен. В этом случае угол поворота a двигателя связан с током через дифференциальное уравнение равновесия моментов на валу

где i – ток якоря – управляющее воздействие; c – коэффициент; Ф – магнитный поток; J – момент инерции якоря и нагрузки, приведённый к валу двигателя;
M_c – момент сопротивления; a – угол поворота вала двигателя – управляемая координата; t – реальное время.

Для простоты дальнейших выкладок примем, что моментом сопротивления можно пренебречь, т.е. M_c = 0. Кроме того, вместо реального времени t введём относительное время 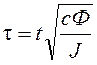. В этом случае уравнение (15) примет вид

Учитывая принятые обозначения: У – управляемая координата, а U – управляющее воздействие, введём замену i = Uи a = Y. С учётом такой замены окончательно запишем уравнение управляемого объекта

Рассмотрим задачу об оптимальном управлении электропривода при минимальных затратах энергии. Функционал (критерий оптимальности) определяется выражением:

Уравнение объекта имеет вид

граничные условия по скорости нулевые

и задана величина отрабатываемого угла

Если ввести обозначения

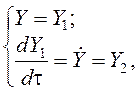
то, (17)-(19) можно переписать