Анализ ПП в цифровых системах управления. Оценка запаса устойчивости цифровых систем управления

Лекция 5.

1. Анализ ПП в цифровых СУ.

2. Устойчивость цифровых СУ.

3. Оценка запаса устойчивости цифровых СУ.

Анализ ПП в цифровых СУ

Модель СУ с цифровым регулятором можно свести к виду:

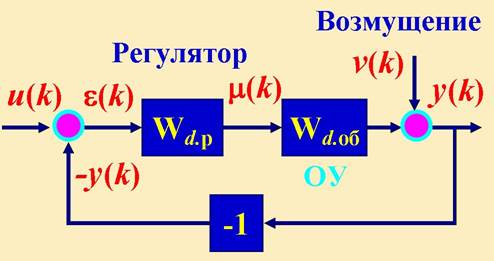
Для этой СУ Z-изображения последовательностей входных u(k), v(k) и выходных y(k) импульсов связаны так:

где

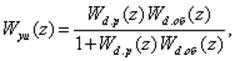
Для определения Z-изображения V(z), приведенного к выходу дискретного ОУ возмущения v(k), которое обусловлено действием на непрерывный ОУ реального возмущения l(t), нужно найти S-изображение приведенного возмущения V(s)

где  W_об.в(s) - ПФ ОУ по каналу возмущения l(t), а L(s) - изображение l(t).

Пример 2. Пусть СУ имеет ОУ- инерционное звено I порядка с ДПФ (см. пример 1)

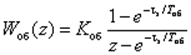
и цифровой И-регулятор с ДПФ

Найдем последовательность y(k) выходных импульсов при ступенчатом возмущении l(t) = l₀·1(t), действующем на ОУ со стороны регулирующего органа.

Тогда

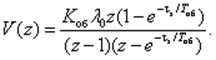
ДПФ замкнутой СУ

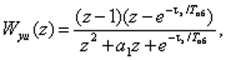
где

Поэтому Z-изображение последовательности y(k) выходных импульсов равно:

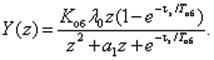
Если взять t_s /T_об = 2 и k_и K_об  =2.092  (это соответствует степени затухания основной компоненты собственных колебаний СУ, равной 0,9), то

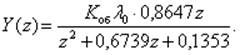
Деление числителя на знаменатель («углом» или программно на ЭВМ) дает следующий ряд:

Числовая последовательность этого ряда равна

Для t_s /T_об = 0,5  и k_и K_об  = 1.01  (степень затухания тоже  равна 0,9) после аналогичных вычислений получим:

ПП в СУ, построенные по этим дискретным значениям выходной величины, показаны ниже.

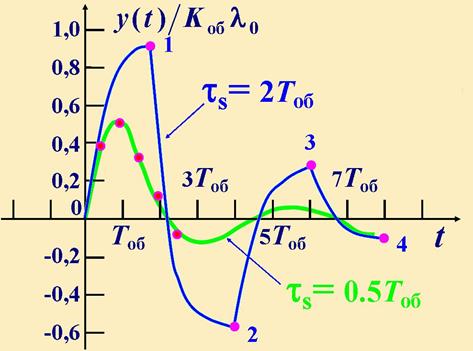
Устойчивость цифровых СУ

Для оценки их устойчивости используются те же критерии, что и для непрерывных СУ.

   Критерий Рауса-Гурвица. 

   Для устойчивости непрерывных СУ нужно, чтобы полюса ПФ замкнутой СУ (корни характеристического уравнения 1 - W_р.с(s) = 0) находились в левой полуплоскости комплексной плоскости. 

Для оценки устойчивости дискретных СУ используют уравнение 1 - W_р.с(z) = 0. Необходимо и достаточно, чтобы все корни уравнения по модулю были меньше 1, т.е. находились на комплексной плоскости z внутри круга  единичного радиуса с центром в начале координат.

Чтобы пользоваться обычными критериями устойчивости Рауса-Гурвица нужно сделать подстановку в характеристическое уравнение z = ( w + 1)/( w - 1) .

Области устойчивости непрерывных

 и цифровых СУ по критерию Гурвица

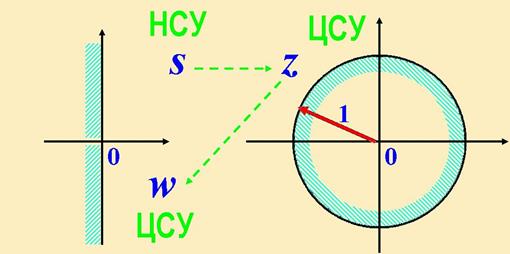
Критерий Михайлова. 

Заменой z= exp ( jt_sw) из характеристического полинома F(z) получают характеристический вектор СУ

Согласно критерию Михайлова дискретная СУ устойчива,  если годограф характеристического вектора, начинающегося на вещественной положительной полуоси при изменении w  от  w = 0   до   w = p/t_s , совершает поворот против часовой стрелки на угол np, проходя последовательно 2n квадрантов комплексной плоскости.

Критерий Найквиста. 

Если отрицательная АФХ разомкнутой дискретной СУ при изменении частоты w  от  w = –p/t_s   до  w = p/t_s  не охватывает точки  –1,  j0 , то СУ, устойчивая в разомкнутом состоянии, сохранит свою устойчивость и после замыкания ее обратной связью.

Если Z-характеристическое уравнение  разомкнутой СУ имеет один корень, равный 1 (что обычно бывает при наличии И-составляющей закона регулирования), то для оценки устойчивости по критерию Найквиста необходимо АФХ  при частоте w = 0   дополнить дугой бесконечно большого радиуса. 

Если дискретная СУ не устойчива в разомкнутом состоянии, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы  отрицательная АФХ разомкнутой СУ при изменении частоты от w = –p/t_s   до  w = p/t_s  kраз охватывала  точку  –1,  j0 ( где k - число корней характеристического уравнения  разомкнутой СУ, расположенных вне окружности единичного радиуса).

Расчет параметров настроек регуляторов
в одноконтурных САР

выполняют следующими способами:

Ä по приближенным формулам;

Ä графо-аналитическим способом на основе АФХ объекта и М-критерия (показателя колебательности);

Ä по расширенным АФХ;

Ä с помощью мат. моделирования.

На практике настройки регуляторов определяют по приближенным формулам, а затем уточняют в процессе настройки САР прямо на ОР.

Оптимальные настройки регуляторов для статических  ОР  первого порядка с запаздыванием для ПП:

1 - апериодического;

2 - с 20%-м перерегулированием;

3 - с  мин ò y²dt  -  приведены ниже.

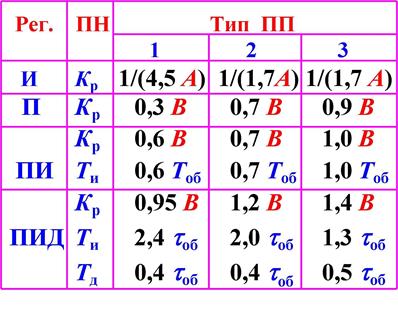
В таблице приняты обозначения:

А = К_об Т_об;

В = Т_об /(К_обt_об).

Более точно настройки определяют по выбранной мат. модели - АФХ  ОР -  с тем, чтобы достигнуть заданного затухания переходного процесса в САР, характеризуемого частотным показателем колебательности  М.

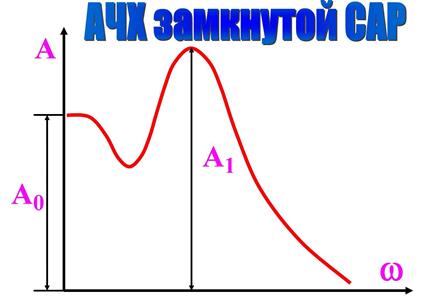
Показатель М равен отношению максимального А₁ и начального А₀ значений АЧХ замкнутой САР  

M  = А₁/А₀.

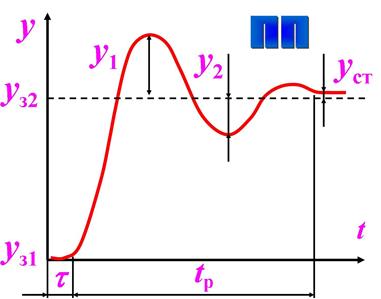
Показатель колебательности M и  перерегулирование h = y₂/y₁ при возмущении по нагрузке связаны между собой следующим образом:

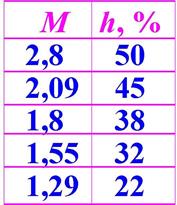
Значение M обычно выбирают в пределах 1,1 - 2,4.

Для типовых ПП M равно:

    1,1 - при апериодическом ПП;

    1,3 - при 20%-м перерегулировании;

    2,1 - при процессе с  min ò y² dt.

Метод графического расчета настроек