Лекция 7.
1. Вычисление Z-ПФ по S-ПФ.
2. Схемы в переменных состояния дискретных СУ.
3. Прямое программирование.
4. Параллельное программирование.
5. Последовательное программирование.
6. Автономное управление в многомерных СУ
Вычисление Z-ПФ по S-ПФ
Это осуществляют двумя методами.
1. Прямой метод.
Вначале по известной ПФ W(s) вычисляют ИПФ h(t) = L-1[W(s)] для дискретных моментов времени kts. Затем находят Z-преобразование для найденной последовательности
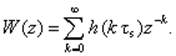
2. Метод вычетов. Z-преобразование для временной последовательности
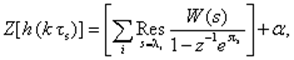
где li - полюса ПФ W(s); вычет (Res) в точке s = li находят по формуле
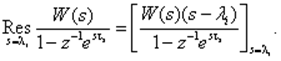
Величину a выбирают так, чтобы
![]()
Пример. Пусть W(s) = 1/(s + a), тогда
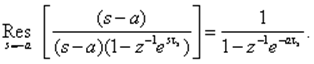
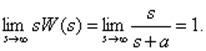
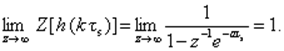
Поэтому a = 0. Следовательно,
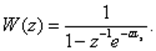
Схемы в переменных состояния для дискретных СУ
Схема СУ в переменных состояния может быть составлена по ПФ опять-таки тремя способами:
1) прямого программирования,
2) параллельного программирования,
3) последовательного программирования.
Схема состоит из прерывателей (дискретизаторов, АЦП), фиксаторов (экстраполяторов), элементов задержки, сумматоров и усилителей.
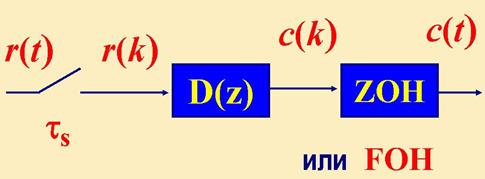
1. Прямое программирование. Пусть ПФ равна
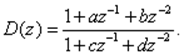
На схеме блоки с коэффициентами aи b включены в прямую связь, с коэффициентами c и d - в обратную отрицательную. Элементы задержки - это блоки z-1, фиксаторы - Н, ключи - квантователи с периодом t.
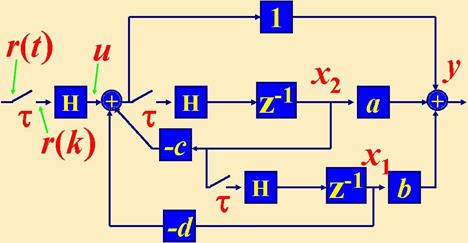
В соответствии со схемой уравнения переходных состояний таковы:
![]()
![]()
![]()
Уравнения переходных состояний описывают изменение координат (переменных состояния) системы в моменты квантования и определяют начальные условия каждого перехода системы в другое состояние.
В
соответствии со схемой системы ДУ состояния ![]()
2. Параллельное программирование. Запишем ПФ в виде суммы дробно-рациональных функций
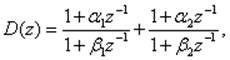 (33)
(33)
где a1, a2, b1, b2 - известные функции от a, b , cи d. Схема системы в ПС , составленная по формуле (33), такова
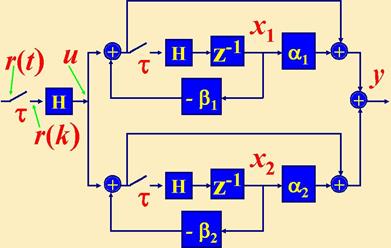
В соответствии со схемой системы уравнения переходных состояний и ДУ состояния:
![]()
![]()
![]()
![]()
3. Последовательное программирование. Запишем ПФ в виде произведения дробно-рациональных функций
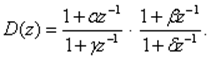 (34)
(34)
В соответствии со схемой системы ДУ состояния
![]()
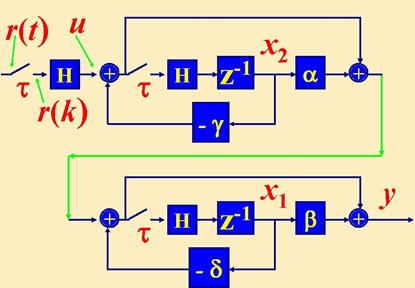
Уравнения переходных состояний:
![]()
![]()
![]()
Автономное управление в МСУ
Качество управления многомерных систем можно повысить, применяя компенсацию (развязывание) перекрестных связей по различным каналам в ОУ. Компенсация может быть статической и динамической.
Первая работает только в статическом режиме, вторая работает также и при ПП.
Пример: рассмотрим МСУ дистилляционной колонной с многократными (четырьмя) отборами.
Выходные величины ОУ – концентрации тяжелого компонента у1, у2, у3. Заданный состав дистиллятов обеспечивается изменением скорости отвода u1, u2, u3 . Для управления используются три одномерных ПИ-регулятора.
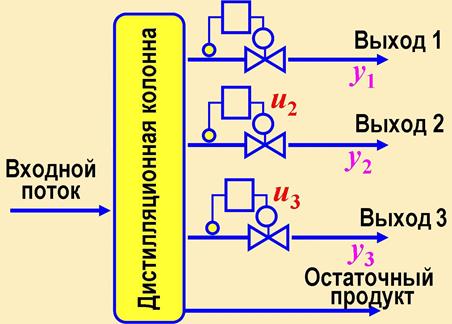
В ОУ присутствуют перекрестные связи только от верхних каналов входа (ui) к нижним каналам выхода (yi). В связи с этим ПФ W(s) ОУ имеет вид
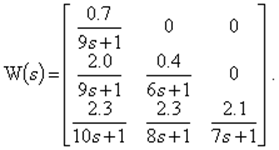 (1)
(1)
Для дистилляционных колонн характерны частые возмущения по заданию. Компенсатор перекрестных связей должен обеспечивать диагональность МПФ замкнутой СУ при возмущениях по заданию как в статике, так и в динамике.
Для этого необходимо, чтобы ПФ компенсатора определялась выражением
![]()
или
![]() (2)
(2)
С учетом (1) при режиме sym- символьных вычислений системы MATLABполучим для динамической компенсации взаимосвязей выражение для ПФ компенсатора
![]() (3)
(3)
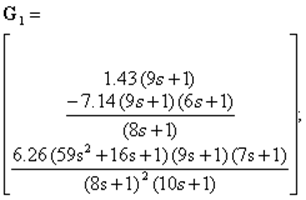
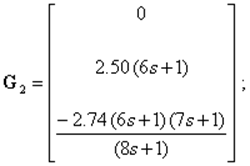
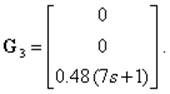
ПФ компенсатора в статическом режиме получим из выражения (3) при s= 0
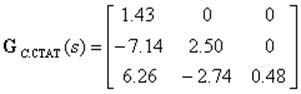 (4)
(4)
Для создания динамического компенсатора перекрестных связей необходимо в выражении (3) в передаточных функциях выделить идеальные дифференцирующие звенья.
Модель МСУ с компенсацией динамических взаимосвязей, созданная в Simulink, показана ниже.
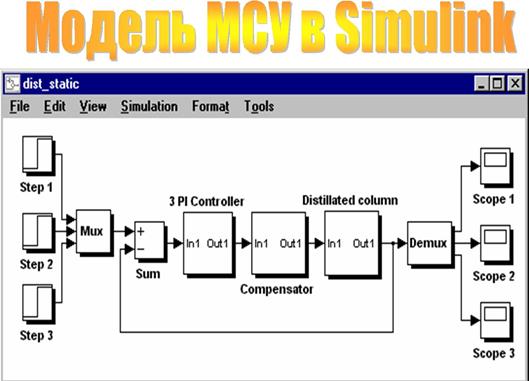
Пусть МСУ имеет многомерный ПИ-регулятор (контроллер) с одинаковыми коэффициентами пропорциональной и интегральной частей - соответственно Kp = 0.25 и Ki = 2.
На входы МСУ подаются сигналы изменения заданий регулятору по входам 1 - 3 с 0 % до соответственно 14, 4 и 10 % от максимального значения выхода по отдельным каналам.
Результаты динамического моделирования работы МСУ без компенсатора, со статическим и динамическим компенсаторами приведены на слайдах ниже. Полный временной диапазон (100%) на графиках соответствует 50 минутам.
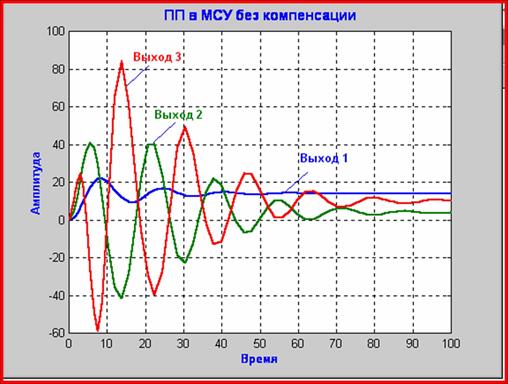
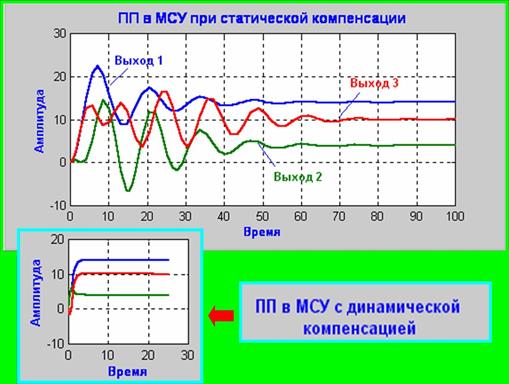
Применение динамической компенсации взаимосвязей позволяет по сравнению с МСУ без компенсации взаимосвязей существенно улучшить качество регулирования, практически устранить динамическое отклонение и сократить время регулирования в зависимости от канала выхода с 40-100 % до 2 % от полного диапазона времени.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.