Дискретные системы. Взвешенная временная последовательность. Z-преобразование, в т.ч. и запаздывания

Лекция 3а.

1. Дискретные системы.

2. Разностные ур-я  “вход-выход”.

3. Взвешенная временная последовательность.

4. Разностные ур-я в переменных состояния.

5. Z-преобразование, в т.ч. и запаздывания.

6. ПФ и АФХ дискретных СУ.

Дискретные системы

В основе современных СУ лежат УВМ и микропроцессорные контроллеры, обмен информацией между которыми происходит в дискретные моменты времени. СУ с такими элементами называют дискретными или непрерывно-дискретными. При этом время tпринимает дискретное множество значений  t_k(k = 0, 1, 2, … ,). Обычно интервал t_s = t_k+1 - t_k = const.

Тогда любой дискретный сигнал будет функцией аргумента k

u(t_k) = u(kt_s) = u(k).

Если для описания непрерывных СУ используют ДУ, то для дискретных СУ - разностные уравнения.

Пусть нужно найти значение выходной переменной у, связанной с входной величиной u соотношением

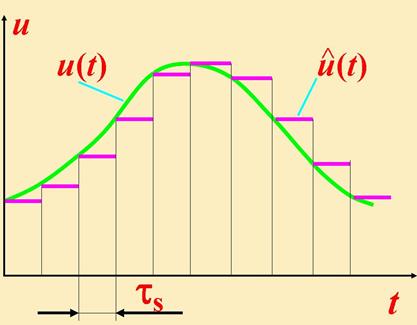
Заменяя непрерывную функцию u(t)  на кусочно-постоянную

,

получим

После манипуляций можно получить разностное уравнение 1-го порядка

Т. о., для определения значения y в последующий момент (k + 1) t_s необходимо запоминать его предыдущее значение в момент y(kt_s ) и значение u(kt_s ) в данный момент.

Линейные дискретные системы можно описать:

–  разностными уравнениями «вход-выход»;

–  взвешенной временной последовательностью;

–  разностными уравнениями в ПС.

Разностные уравнения  “вход-выход”

Линейное уравнение имеет вид

                                    (4)

Число y(k) - выход  в момент kt_s (шаг дискретности t_s для простоты описания формул обычно опускают).

Числа y(k-1), y(k-2) - предыдущие значения выхода, запоминаемые в памяти ЭВМ. Числа u(k) , u(k-1) - значения входа в моменты k, (k-1), также запоминаемые в ЭВМ.

Уравнение  (4) -  рекурсивное или разностное уравнение. Оно  позволяет  вычислять каждое последующее значение выхода системы по предыдущим данным.

Взвешенная временная последовательность

Это аналог импульсной переходной функции для дискретных систем. В них на вход вместо дельта-функции, а подают дельта-последовательность (Д-П) Кронекера

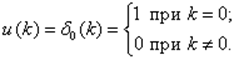
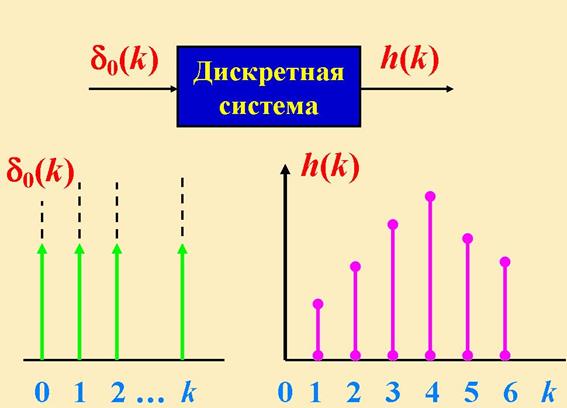
Приняв в (4) u(k) = d₀(k) и обозначив реакцию системы через h(k), получим выражение для взвешенной временной или весовой последовательности

Вычисления h(k) начинают с k = 0,

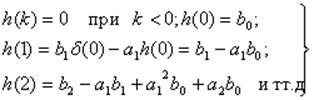                                                                                               (6)

Пусть на вход подана Д-П

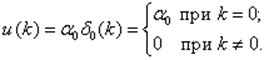
Тогда    y⁰(k) = a₀h(k),    где  y⁰(k) - взвешенная (множителем a₀) реакция системы на Д-П, приложенную в момент   k = 0. Реакция системы y1(k) на Д-П, приложенную в момент k = 1.

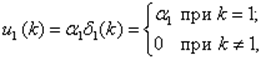
будет равна y(k) = 0  при k < 1;

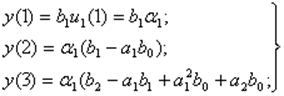                                                                                                    (7)

и т.д.    

Сравнивая (6) и (7), получим

y¹(k) = a₁ h(k-1).

 Если Д-П приложена в момент k = j, а

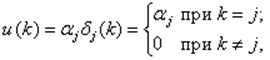
то реакция системы

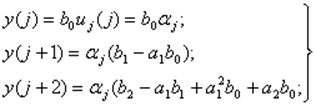                                                                                               (8)

и т.д. 

Пусть подана сумма Д-П, приложенных в моменты  k = 0, 1, 2, … ,

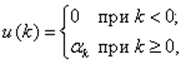
или

 

Тогда на основе принципа суперпозиции выход системы будет равен сумме реакций от входов u(0), u(1), u(2), … 

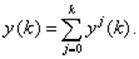
Или с учетом (8)

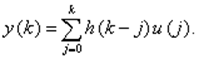                                                           (9)

Произведя замену m = (k - j), получим аналог интеграла свертки для непрерывных систем

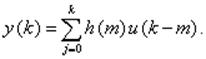                                                       (10)

Разностные уравнения в переменных состояния

Для дискретных систем вместо ДУ используют разностные уравнения c шагом дискретности t_s , который обычно опускают, при х(0) = х₀

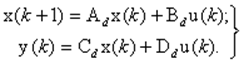                                                 (11)

Этому уравнению соответствует схема в переменных состояния

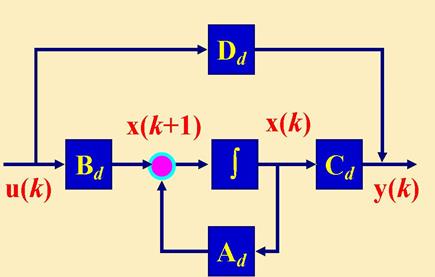
Решение уравнения (11) получим, подставляя k = 0, 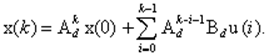1, 2, … .

                                                                                                    (12)

Матрицу   j(k) = А_d^k- называют фундаментальной или переходной матрицей.Подставим  j(k) в (12) и получим