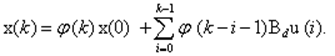Дискретные системы. Взвешенная временная последовательность. Z-преобразование, в т.ч. и запаздывания, страница 2

                                                                                         (13)

Первый член зависит только от начальных условий х₀ , второй - только от воздействия u_i . Выход системы согласно (11) и (13) равен

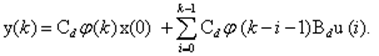                                                                                  (14)

Для системы, описываемой разностными уравнениями в переменных состояния, можно найти взвешенную временную последовательность, т.е. реакцию системы h(k) при нулевых начальных условиях x(0) = 0 и входе в виде Д-П

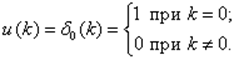
Последовательно решая уравнения (11) при D_d = 0, k= 0, 1, 2, … , получим

 

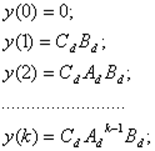
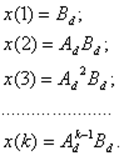
Т. е.

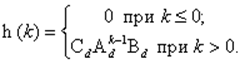                                                                                                         (15)

Z-преобразование

Оно сводит решение разностных уравнений системы к алгебраическим операциям и устанавливает соответствие между функциями дискретного времени и функциями комплексного переменного z. Для последовательности f(k) при положительных k используют одностороннее Z-преобразование, для положительных и отрицательных k- двухстороннее.

Они имеют вид

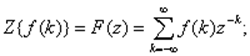
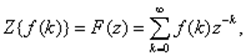
Обратное преобразование находят по формуле

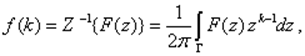
где Г - замкнутый контур в z-плоскости, обычно окружность единичного радиуса с центром в начале координат;

 z = exp (t_ss).

Для упрощения вычисления дискретной ПФ (ДПФ) используют приближенные формулы.

Простейшее преобразование осуществляют с помощью формулы

s = (z - 1) / t_s z.                             (16)

Более точный переход к ДПФ  -  с помощью аппроксимации Тастина (Tustin) - билинейной аппроксимации

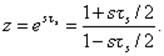
ДПФ W_d(z) из непрерывной ПФ W(s) получается подстановкой

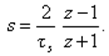                                                                 (17)

Замена (16) соответствует численному интегрированию по методу прямоугольников, подстановка (17) - по методу трапеций.

          Для обеспечения соответствия между непрерывным  и дискретным частотным откликом  на частоте w

используют аппроксимацию Тастина   с модифицированной  частотой

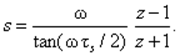                                                      (18)

В справочной литературе приводятся таблицы Z-преобразования и модифицированного Z-преобразования

Z-преобразование запаздывания

В ОУ с запаздыванием сигнал, модулирующий последовательность импульсов, может запаздывать  точно на целое число периодов t = rt_s .

В этом случае ДПФ ОУ W_t(z) будет равна ДПФ ОУ W0 (z) без запаздывания, умноженной на z^-r

Если запаздывание составляет только часть периода квантования t = λt_s 
( 0 < λ  < 1) , то формула одностороннего Z-преобразования меняет свой вид

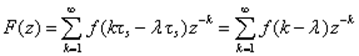
Для удобства расчетов вводят параметр с = 1 - λ . Тогда

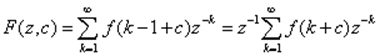
Для нахождения F(z,c) существуют  таблицы модифицированного Z-изображения.

В общем случае при произвольном запаздывании находят число rцелых периодов квантования на интервале t и параметр с из соотношения

Тогда ДПФ ОУ с запаздыванием будет равна

Примеры модифицированного Z-преобразования

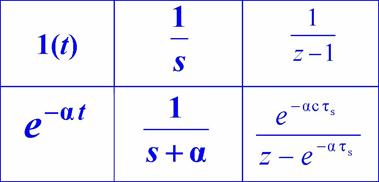
ПФ и АФХ дискретных СУ

Применяя преобразование Лапласа к (4) и проводя замену z= exp (t_ss), получим ДПФ системы в общем виде

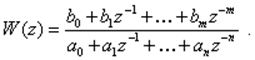
Умножая числитель и знаменатель на z  в положительной степени, равной наибольшей отрицательной степени,  получим ДПФ в привычном виде

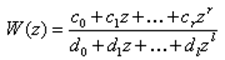
Частотные характеристики дискретных систем получают из ДПФ заменойz= exp (jtsw).
Эти характеристики являются периодическими функциями частоты с периодом

ws = 1/ (2tps):

Пример 1. В СУ есть дискретный ОУ - непрерывный ОУ и ЦАП (ZOH) с ПФ

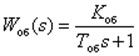
Из таблиц Z-преобразования ДПФ ОУ

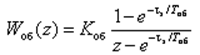
Тогда АФХ дискретного ОУ равна

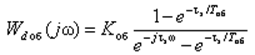
Из этого выражения можно найти  АЧХ и ФЧХ дискретного ОУ. Задавшись значением

получим АФХ

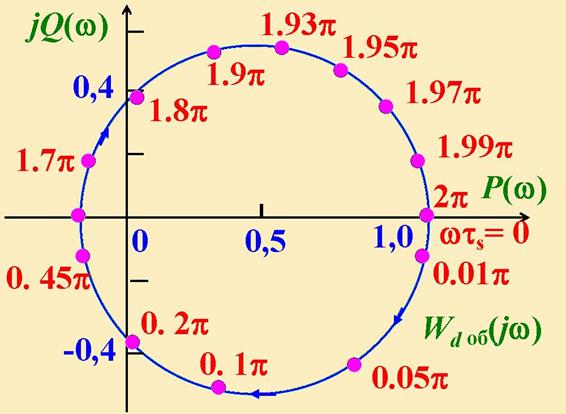
Если непрерывный ОУ имеет запаздывание, содержащее целое число r периодов квантования t = rt_s, то его ДПФ

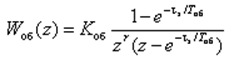
Если запаздывание ОУ t, не является кратным периоду квантования t_s, то необходимо использовать модифицированное Z-преобразование. Тогда

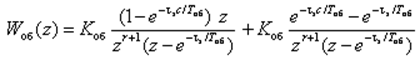
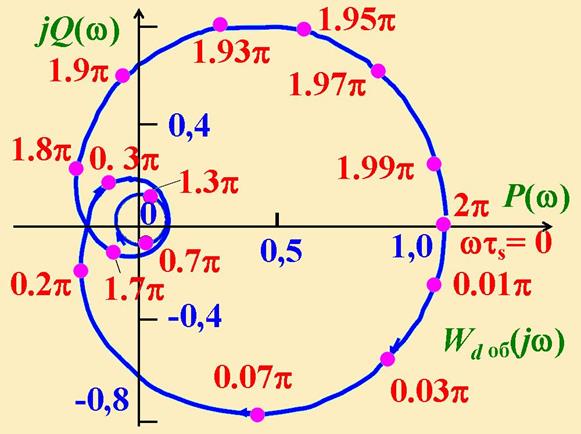
где r- целое число периодов квантования. АФХ ОУ с запаздыванием