Теория графов

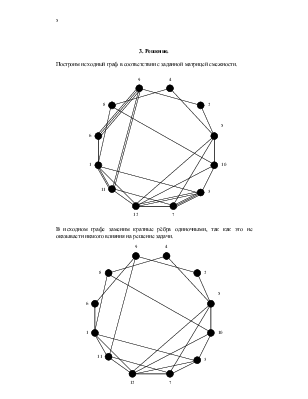
1. Теоретическая часть.

Граф G(X,Y) – множество вершин X и множество рёбер Y, соединяющих эти вершины.

Граф G(X,Y) планарный, если его рёбра пересекаются лишь в его вершинах.

Граф G(X,Y) плоский, если его можно сделать планарным.

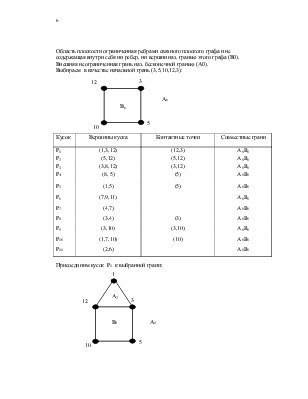
Область плоскости, ограниченная ребрами плоского связного графа и не содержащая внутри себя ни ребер, ни вершин, называется гранью.

Две вершины графа называются смежными, если существует соединяющее их ребро.

Ребро называется инцендентным двум вершинам, если оно связывает эти вершины.

Два ребра называются смежными, если существует вершина инцендентная обоим рёбрам.

Если в графе любые две вершины соединены более чем одним ребром, то такой граф называется мультиграфом. Рёбра, соединяющие одну и ту же пару вершин, называются кратными. Наибольшее число кратных рёбер, соединяющих какую-либо пару вершин называется мультичислом.

Ребро, у которого обе вершины совпадают, называется петлёй.

Граф, у которого между любыми двумя различными вершинами существует одно ребро, называется полным графом.

Количество рёбер, инцендентных какой – либо вершине, называется локальной степенью этой вершины.

Последовательность рёбер, заданная парами вершин вида ((x₀,x₁), (x₁,x₂), … (x_i-1,x_i), …), в которой два соседних ребра смежные, называется маршрутом. Если все рёбра в маршруте различные, то такой маршрут называется цепью. Цепь, в которой совпадают начальная и конечная вершины, называется циклом.

Вершины называются связанными, если они могут быть соединены  произвольным маршрутом.

Граф называется связным, если любые две его различные вершины связанные.

Связной граф без циклов называется деревом.

Для плоского графа с n вершинами, r рёбрами и f  гранями справедлива формула Эйлера:

n – r + f = 2.

Пусть граф G(X,U) – граф без петель и кратных рёбер. Раскраской вершин графа G(X,U) называется такое разбиение множества его вершин Х на P непересекающихся подмножеств X₁,…,X_p, таких, что

U = U u_i  и  X_i W X_j = Æ. При этом, каждое подмножество X_i не содержит смежных вершин.

При раскраске вершин графа любая пара смежных вершин раскрашивается в различные цвета.

Наименьшее количество красок, необходимых что бы раскрасить заданный граф, называется его хроматическим числом.

Наименьшее число рёбер, после удаления которых в графе не остаётся ни одного цикла, называется цикломатическим числом g.

g = r – n + p, где

r – число рёбер,

n – число вершин,

p – число компонент связности.

Критерий оценки плоского графа.

Если количество рёбер r > 3(n – 2), то граф не плоский.

Если количество рёбер r ≤ n + 2, то граф плоский.

Если n + 2 ≤ r < 3(n – 2), то требуется дальнейшее исследование.

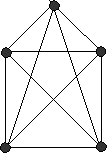
Теорема Понтрягина – Куратовского.

Необходимые и достаточные условия, при которых граф является плоским, состоят в том, что граф не должен содержать частичных подграфов типа I и II.

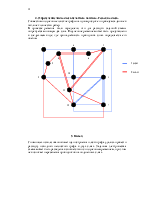
2. Анализ задания.