Теория графов, страница 2

Для заданного графа имеем:

Количество вершин n = 12;

Количество рёбер     r = 20

По критерию оценки получаем: 14 < 20< 30 (неопределенность).

Необходимы дополнительные исследования.

Применяем теорему Понтрягина – Куратовского.

В исходном графе содержится подграф I типа.

<рис>

Следовательно, исходный граф не является плоским, значит, не получится провести разводку линий связи в одном слое. Для определения числа слоев используем алгоритм построения плоского изображения.

3. Решение.

Построим исходный граф в соответствии с заданной матрицей смежности.

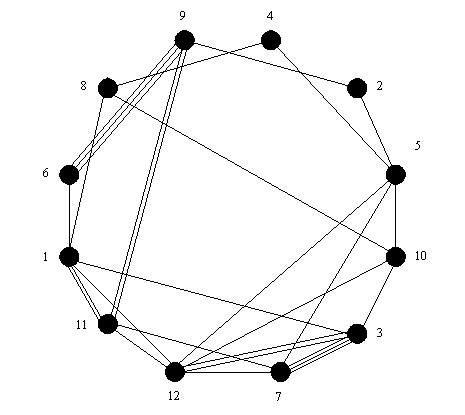
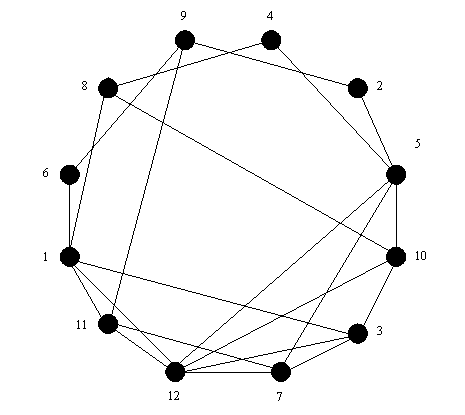
В исходном графе заменим кратные рёбра одиночными, так как это не оказывает никакого влияния на решение задачи.

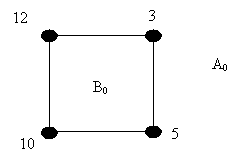
Область плоскости ограниченная ребрами связного плоского графа и не содержащая внутри себя ни ребер, ни вершин наз. гранью этого графа (В0). Внешняя неограниченная грань наз. бесконечной гранью (А0).

Выбираем  в качестве начальной грань (3,5,10,12,3):

 

Кусок	Вершины куска	Контактные точки	Совместные грани
P1	(1,3,12)	(12,3)	A0B0
P2	(5,12)	(5,12)	A0B0
P3	(3,8,12)	(3,12)	A0B0
P4	(8, 5)	(5)	A0B0
P5	(1,5)	(5)	A0B0
P6	(7,9,11)		A0B0
P7	(4,7)		A0B0
P8	(3,4)	(3)	A0B0
P9	(3,10)	(3,10)	A0B0
P10	(1,7,10)	(10)	A0B0
P11	(2,6)		A0B0