Применение основных теорем динамики к исследованию движения материальной точки

Применение основных теорем динамики к исследованию движения материальной точки.

Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которого расположена в вертикальной плоскости. Найти скорость шарика в положении В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках пренебречь.

Дано:

m = 0.5 кг;

V_A = 2 м/с;

  = 1,5 с;

R = 4 м;

f = 0.25;

= 20^о;

 = 60^о.

Определить: V_В , V_c , N_c , V_D.

Решение.

1)  Рассмотрим движение шарика на участке АВ. В данном участке АВ, шарик движется внутри трубки по окружности радиусом R.

а) Определим длину участка АВ:

м.

б) Так как мы нашли длину участка АВ то для определения скорости шарика в точке В воспользуемся теоремой об изменении кинетической энергии:

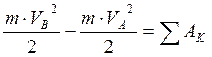
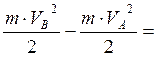
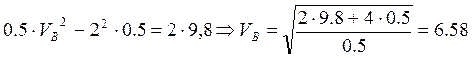 м/с.

2)  Рассмотрим движение шарика на участке АС.

а) Определим длину участка:

м.

б) Так как мы нашли длину участка АС то для определения скорости шарика в точке С воспользуемся теоремой об изменении кинетической энергии материальной точки:

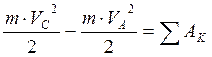
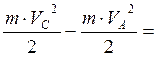
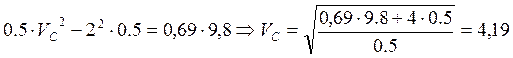 м/с.

3)  Рассмотрим скорость шарика на участке ВD. Так как нам известно время движения шарика на данном участке, то в качестве решения, по нахождению скорости, принимаем теорему об изменениях количества движения:

Ось Х направлена вдоль участка ВD.

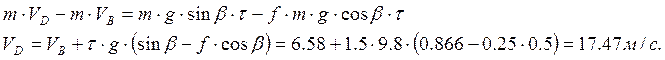
4) Определим давление шарика на стенку трубки в положении С. Как известно давление перпендикулярно к направлению движения, то через вектор давления проведем ось Х_с.

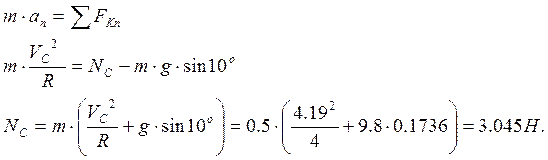
 Ответ: V_B= 6.58 м/с; V_D = 17,47 м/с; V_C = 4.19 м/с; N_C = 3.045 Н.