Определение параметров вращения судна по определениям координат одной антенны

1. ОПРЕДЕЛЕНИЕ    ПАРАМЕТРОВ    ВРАЩЕНИЯ    СУДНА

ПО  ОПРЕДЕЛЕНИЯМ  КООРДИНАТ  ОДНОЙ  АНТЕННЫ

Рассматривая в соответствии  с  положениями  кинематики  (см.,  например,

 / Иродов/) судно как тело сложной формы,  при недостаточной определенности  законов и параметров его движения на морском волнении  в общем случае необходимо учитывать,  что судно  при качке и остановленном движителе  может совершать вращательное движение  как вокруг некоторой точки,  так и  вокруг некоторой оси.

В первом случае  антенна  судового ПИ ССРНС, которую рассматриваем как точечный объект, будет перемещаться  по поверхности  сферы с радиусом R_п,  центр которой - точка  с координатами X_ц, Y_ц, Z_{ц .}

Во втором антенна  судового ПИ будет перемещаться  по окружности с радиусом R_п,  центр которой  с координатами X_ц, Y_ц, Z_ц  расположен на оси вращения судна.

 При решении задачи по определению оценок  координат  X_ц, Y_ц, Z_ц    центра перемещения и его  радиуса   R_п полагаем известными   координаты x_j, y_j, z_j    точек    j = 1…n  перемещения  антенны.

1.1. Определение координат  центра  и радиуса перемещения

антенны по сферической поверхности

1.1.1. Координаты    центра и радиус  перемещения антенны по сферической поверхности   могут быть определены по  алгоритму, для составления которого  воспользуемся  уравнением для точки на  сфере  в виде

                                                                              ( 1 )

Для  использования при определении искомых координат  всего массива точек  траектории кругового перемещения антенны составим функционал

                                      ( 2 )

Представим  уравнение для точки на сфере в виде

где      

Минимизируя   функционалL_s   по  искомым  величинам       

 получим  систему  из  четырех уравнений

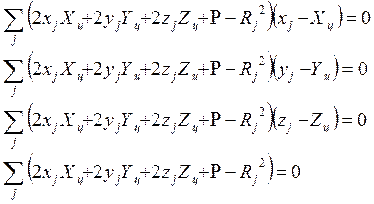
Так как  четвертое уравнение системы равно нулю,  то  и вторые  составляющие (результатов перемножения на вторую скобку) первых трех  уравнений  равны соответственно

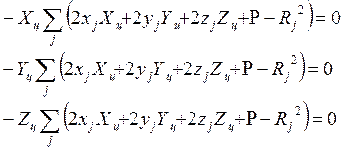
После соответствующих преобразований  система  из  четырех уравнений относительно неизвестных может быть  представлена в виде:

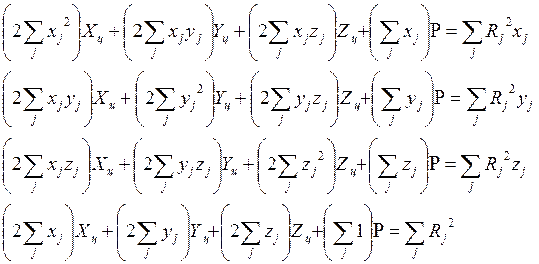                                   ( 3 )

Радиус перемещения антенны по сферической поверхности после определения величины     может быть рассчитан  по формуле

1.1.2.  В частном случае,  когда  определение  радиуса   не представляется необходимым,  определение только координат  центра перемещения  антенны по сферической  поверхности может быть  осуществлено решением системы  из трех уравнений, которую получим,  подставляя  в   три верхние  уравнения  системы  параметр ,  который  найдем из  четвертого уравнения 

                                  ,

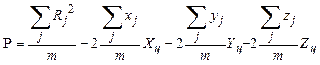где  ,  после соответствующих преобразований систему из трех уравнений

получим             

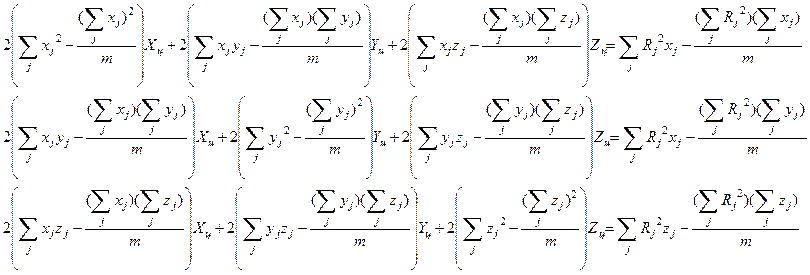
Обозначая  ,   ,    ,   , представим систему уравнений  в виде:

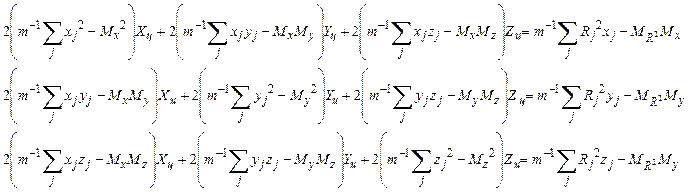         ( 4 )

Результаты расчетов для определения  координат     центра, относительно которого антенна перемещается по сферической поверхности,при  решении систем уравнений  ( 3 )  и ( 4 )  оказались одинаковы, а их отличия    от  истинных  значений  указанных параметров  находились в  пределах  статистической погрешности.  Однако эти  расчеты производились в конце июня  и  июле. Первоначальное (конец мая и начало июня) использование системы уравнений  ( 3 )    для  нахождения  оценок       при  перемещении  антенны  вокруг  оси вращения,  когда  и  точки  траектории перемещения антенны и центр ее перемещения  расположены в одной плоскости,  давало  результаты  в несколько раз отличавшиеся от истинных величин.  Это обусловило необходимость получения систем уравнений,   одним  из которых  является  уравнение  плоскости  перемещения антенны.

.

1.  2. Определение параметров плоскости

         кругового перемещения антенны

Для  составления уравнения             плоскости,  в которой располагается орбита кругового перемещения антенны,  достаточно располагать  координатами трех точек (1, 2 и 3),  где (см., например, / 1 /)

                                                                                        ,                           

  ,      ,      ,          

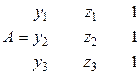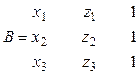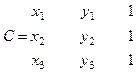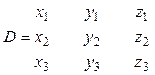
 и  определить  параметры нормального уравнения  плоскости,  которое представим    в виде:   

                                             ,                                                          ( 5 ) 

где             ,                                 

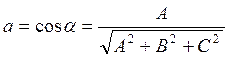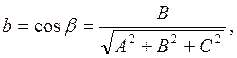
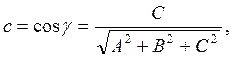
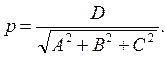
 С целью минимизации погрешностей,  обусловленных в определяемых параметрах воздействием случайных помех, целесообразно получить по методу наименьших квадратов алгоритм,  в котором при определении искомых  величин  использовались  бы  координаты всего массива точек  на траектории перемещения. Для  этого составим функционал:

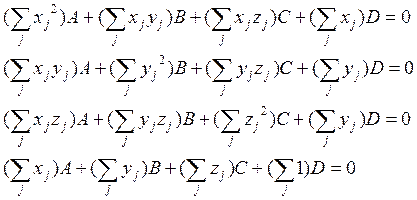Для ее решения  допустим,  что  параметр C=С₁  известен и равен  1. Тогда, используя три верхних уравнения, составим   систему уравнений относительно неизвестных

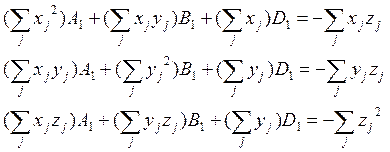Найденные при ее решении  величины будут  равны

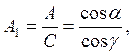
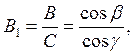
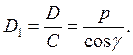
Учитывая,  что   ,  определим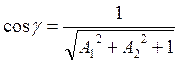   

и                            

1.3. Определение координат  центра  и радиуса перемещения

  антенны  в  плоскости  вокруг оси вращения