Определение параметров вращения судна по определениям координат одной антенны, страница 2

Решение системы уравнений (найденной в середине мая),  составленной на основе  общих представлений  высшей алгебры   (например, / Курош /) из  трех  верхних  уравнений  системы    ( 3 )  и четвертого  уравнения  ( 5 ),  позволило определить   искомые  параметры     с  погрешностью,  соответствующей заданным статистическим  параметрам  погрешностей  измеряемых  координат  антенны.  Однако требование достаточного  математического обоснования   получаемых  зависимостей обусловило необходимость  поиска и  проверки  других  способов  решения задачи.     Ниже  дается их  изложение  в  последовательности,  соответствующей  степени  математической обоснованности.

1.3.1.  Для  составления системы уравнений по методу множителей  Лагранжа  составим  функцию

                           ( 6 )

в виде  суммы  функционала  ( 2 )  и  уравнения  ( 5 )  плоскости в нормальной форме,  умноженной  на  неизвестный  параметр .  Четыре  уравнения исходной  системы  получим,  минимизируя  функцию  ( 6 )  по  параметрам        .   Пятое  -  уравнение  ( 5 )  плоскости в нормальной форме.

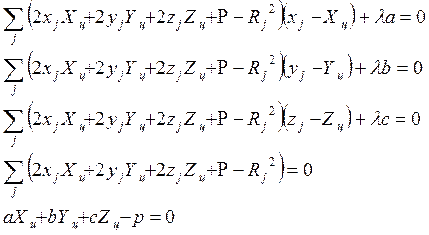
Произведя  в  четырех  уравнениях системы  преобразования,  описанные  в 1.1,  получим систему  уравнений

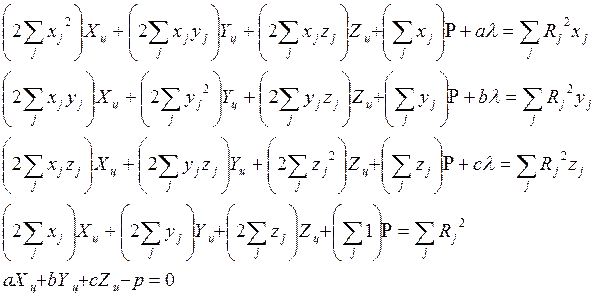                          ( 7 )

При необходимости определения только координат центра  кругового перемещения антенны  после преобразований,  рассмотренных также в 1.1,  можем  получим систему  уравнений

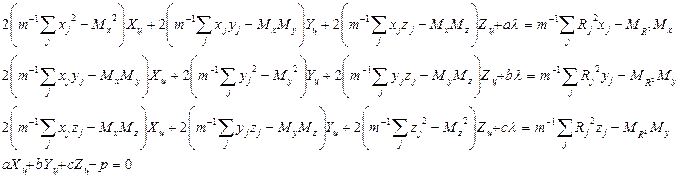                ( 8 )

Результаты расчетов для определения  координат     центра, относительно которого антенна вокруг оси вращения перемещается по круговой орбите,при  решении систем уравнений  ( 7 )  и ( 8 )  оказались одинаковы, а их отличия    от  истинных  значений  указанных параметров  находились в  пределах  статистической погрешности. 

1.3.2.  Более простые системы уравнений для нахождения оценок  координат    центра и радиуса  перемещения антенны  могут быть  получены  при составлении минимизируемой функции  ( 6 )   по  методу,  обоснованному  в  / Смирнов В. И. /.  Для этого,  используя уравнение плоскости    ( 5 ),   выразим  один  из определяемых  параметров (например,  )  через  другие.

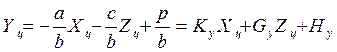
Тогда  функционал   ( 2 )  будет  получен в виде

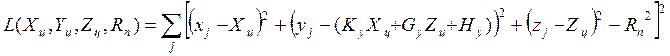                  ( 9 )

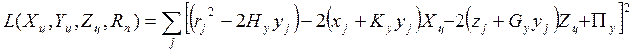         ,       ( 10 )

где        ,            .

Минимизируя  функционал ( 10 ) по параметрам     ,  получим  систему  из  трех  уравнений         

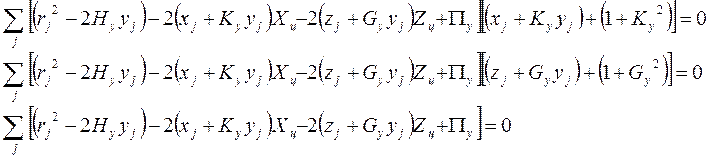                                                               ,   ( 11 )

которая  после  преобразований   будет иметь  вид:

,   (12 )

так как   при равенстве нулю  третьего   уравнения в  ( 11 )  верны равенства:  

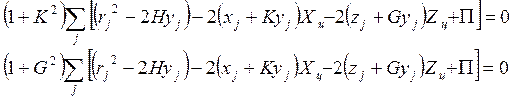
Выразив при использовании уравнения  ( 5 )  параметр   через  другие, получим 

                                       .

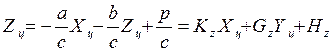Подставляя  параметр    в функционал  ( 2 )  и  произведя  описанные выше преобразования,  получим  аналогичную  ( 12 ) систему  уравнений

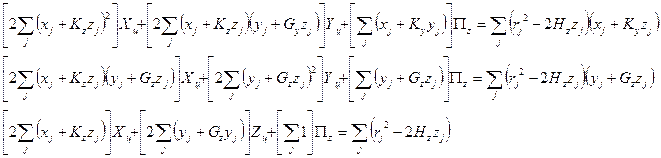.     ( 13 )

Ее решение  позволяет определить оценку  и  координаты  .

1.3.3.  Представляется соответствующим сути  метода Лагранжа  использование   функционала 

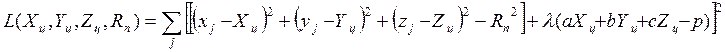.    ( 14 )

Минимизируя его  по     ,  получим  систему    

                                  ,

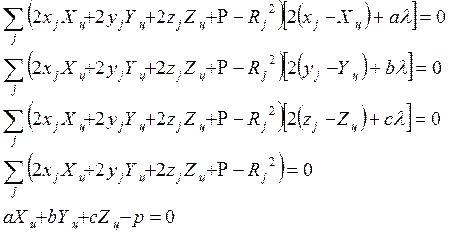которая  с очевидностью  преобразуется  в систему   (  15  ),  так  как в соответствии  с  показанным в   1.1 

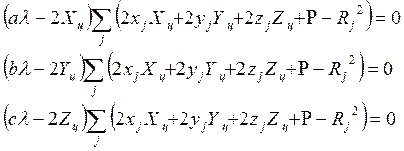
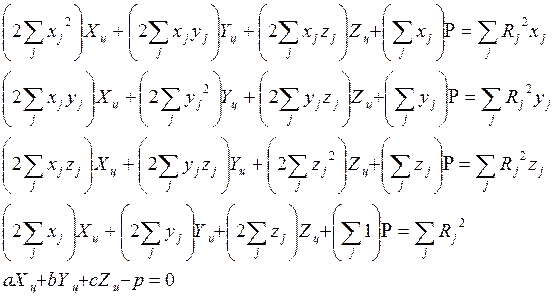.        ( 15 )

Для определения четырех неизвестных       в системе   достаточно использовать четыре  уравнения.   Получить  ее  с обязательным использованием уравнения  плоскости (при  перемещении антенны по круговой траектории)  можно любым известным  из основ высшей математики способом.    

Примечание.

При допущении, что в реальных условиях может быть неизвестным перемещение антенны по сферической поверхности или  по круговой  орбите, точки  которой расположены в плоскости совместной с центром перемещения,  возникает  задача выбора  одной из двух соответствующих  систем  уравнения.  При неверном выборе     определение искомых  параметров возможно с недопустимыми  погрешностями.