Определение параметров вращения судна по определениям координат одной антенны, страница 3

Решение как  данной задачи, так и  определение  параметров вращательного движения судна при его перемещении  обуславливает  необходимость  получения  и использования данных о координатах  двух точек движущегося тела  (судна),  т. е.  координатах двух судовых антенн  ПИ ССРНС.

 Возможности  использования координат  двух антенн и угловых параметров судна  рассматриваются в следующем  разделе.

2.  ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ОСИ  И  ЦЕНТРОВ       КРУГОВОГО   ПЕРЕМЕЩЕНИЯ    АНТЕНН  АП ССРНС НА  ДВИЖУЩЕМСЯ  СУДНЕ  

2.1.  Модель предполагаемого движения  судна

Полагаем, что  независимо от сил, действующих на судно при качке,  точки a и o, в которых установлены судовые антенны,   совершают  одновременно  и  поступательное  и вращательное движения. Вместе с осью, все точки которой движутся поступательно,  совершают поступательное движение  и антенны, но при качке  они одновременно  перемещаются и по круговым траекториям вокруг общей оси вращения.  При  нахождении центров кругового перемещения антенн на общей оси координаты  центров различны.

Векторы    и  (см. рис.  2.1) в неподвижной координатной системе   начальный момент    представим в виде  

                        ( 1 )

В  последующие (i-е)  моменты времени  векторы  представим  в виде

        ,              ( 2 )

где  

                               

                                            ( 3 )

              ( 4 )

Очевидно, что при  только поступательном движении  судна  приращения  координат    ,  ,  обусловленные  им,  будут  одинаковы  для  всех его точек.    Составляющие  

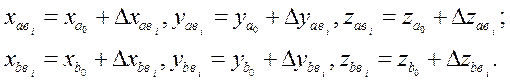                   ( 5 )

координат   (3)  и  (4)  обусловлены    перемещением антенн, установленных   в точках  aи b,  вокруг  их общей  оси вращения. 

2.2.   Определение  направляющих  косинусов  оси  вращения

Оценим вначале  возможность определения  направляющих косинусов оси,  вокруг которой поворачиваются  две антенны,  на судне  при отсутствии  поступательной составляющей его движения.  Для  этого  составим уравнения  двух плоскостей,  в которых  расположены точки a и o  перемещающихся  антенн.

                                                  (6)        

                                                    (7)

Разделим уравнения   (5)  и  (6)  на  соответственно     и   ,  получив  уравнения  

                                                (8)

                                                  (9)

По условию параллельности плоскостей

                       ,      ,

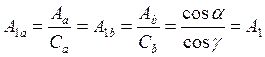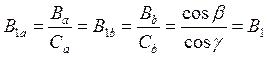   но  .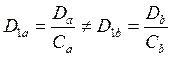

Вычитая  ( 8 ) из  ( 7 ),  получим

                    ,            (10)

где                .

Далее,  в соответствии с  используемыми  в  1.2  приемами,  составим функционал

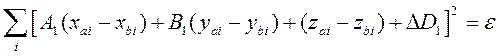              .            (11)

Минимизируя  функционал  (11) по  параметрам  ,  , ,  составим систему уравнений

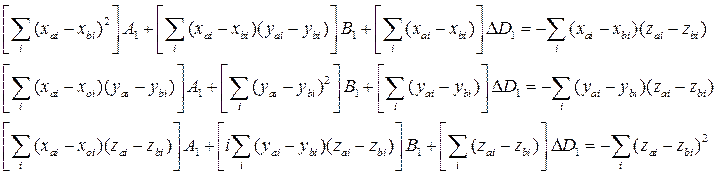. (12)

Учитывая, что

 ,     ,   ,

где   -  модуль расстояния  между точками    и   ,  система   (12) может быть представлена в виде 

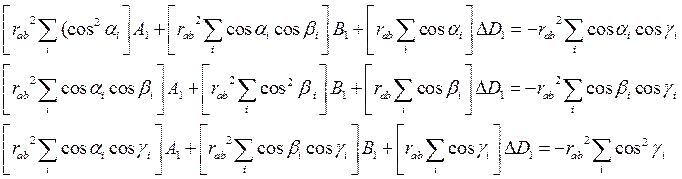   (13)

Найденные при ее решении  величины будут  равны

                                                 

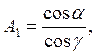
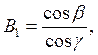
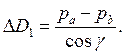
Учитывая,  что   ,  определим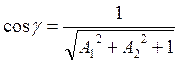   

и                            

Геометрический  смысл  разности      в том,   что  она,  являясь кратчайшим расстоянием   между  плоскостями,   является и  расстоянием между центрами  поворота антенн.  Следовательно, при известных координатах   одного из центров поворота  антенн и определении  направляющих косинусов  она  может быть использована для расчета координат  и второго центра поворота антенны.

Нетрудно убедиться, что  при вычитании координат  ( 4 )  из   ( 3 ),  в которых учтены составляющие поступательного движения, в их  разностях  эти составляющие взаимно компенсируются.  Следовательно, полученные  зависимости  пригодны и для  определения параметров оси вращения  антенн  и на поступательно движущемся судне.

2.3.   Определение  угла  поворота антенн

            вокруг оси кругового  перемещения