Для этого расчетные формулы следует разместить в строке электронных таблиц, поскольку необходимые коэффициенты (bj) и индексы (j) тоже размещены в строках (индексы j являются заголовками соответствующих столбцов).
Для конкретности допустим, что необходимо вычислить изменение энтальпии при нагреве одного моля воды от температуры 298.15 К до температуры кипения – 373.15 при нормальном давлении. Считаем, что необходимые данные присутствуют на листе электронных таблиц (рис. 5, строка 10). Расчет выполним в строке 12, но предварительно, например, в столбце «А» со строки 11 разместим значения температур. Занесем в ячейку А11 значение 298.15, а в ячейку А12 – значение 373.15. Для организации расчета в ячейку С12 введем формулу
[=C9*(($А12^(C$1+1)-$A11^(C$1+1))/(C$1+1))].
Для создания «жестких ссылок» (знак $) следует использовать клавишу F4. Нажимая ее несколько раз, можно получить требуемую комбинацию знака $, буквы обозначения столбца и номера строки. Именно она обеспечивает наименьшую работу при последующем копировании и редактировании формул в ячейках, что должно стать понятным из дальнейшего изложения.
Обратите внимание, что это выражение совпадает с окончательным выражением (3) под знаком суммы, если учесть, что допустимо записать следующие соотношения:
bj = C9,
j = C1,
T1 = A11,
T2 = А12
и понимать их как утверждения, что содержимое указанной ячейки представляет соответствующую величину. Таким образом, в ячейке С12 должен получиться результат, представляющий первое слагаемое в выражении суммы в формуле (3).
Электронные таблицы устроены таким образом, что, если скопировать любым способом ячейку С12 и вставить результат копирования в соседнюю в ряду ячейку (D12), то адреса ячеек (точнее, буквы в обозначении столбцов) в формуле изменятся на величину смещения, кроме тех букв, перед которыми стоит знак $, запрещающий их изменение при копировании:
[=D9*(($А12^(D$1+1)-$A11^(D$1+1))/(D$1+1))].
Легко заметить, что изменились значения j и bj, а ссылки на температуры Т1 и Т2 остались прежними. Таким образом, без особых усилий в ячейке D12 оказалось второе слагаемое суммы в формуле (3). Если копии ячейки С12 вставить во все ячейки в ряду, вплоть до G12, то будут вычислены все слагаемые. Для вычисления изменения энтальпии при нагреве воды от температуры 298.15 до 373.15 К остается только найти их сумму. Например, в ячейку I12 ввести функцию [=СУММ(С12:G12)] – в ней и получится искомое значение.
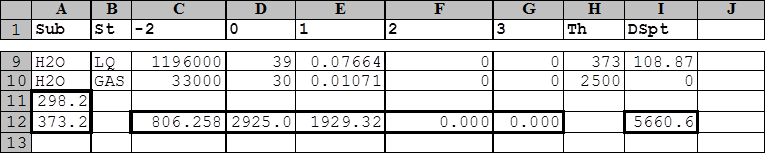
Рис. 7. Результаты непосредственного расчета на листе электронных таблиц изменения энтальпии одного моля воды при ее нагреве от 298.15 К до 373.15 К
Если изменить условие задачи и попытаться найти изменение энтальпии воды при ее нагреве до температуры кипения (Tкип) и превращения в пар при той же температуре, то для этого достаточно учесть изменение энтальпии (DHисп) при испарении воды:
![]() (4)
(4)
где DSисп – изменение энтальпии при испарении одного моля воды. Это значение имеется в базе данных в столбце под названием DSpt (ячейка I9). Поэтому для получения нового решения достаточно в ячейку Н12 ввести формулу [=H9*I9] и изменить формулу в ячейке: [=СУММ(С12:Н12)]. Результат вычислений представлен на следующем рисунке.

Рис. 8. Результаты расчета на листе электронных таблиц изменения энтальпии воды при ее нагреве от 298.15 К до 373.15 К с последующим превращением в пар при той же температуре
Снова изменим условия задачи и сформулируем ее так: определить изменение энтальпии Н2О при нагреве от температуры 298.15 до 2000 К.
По существу новое условие означает, что в дополнение к предыдущему решению надо вычислить изменение энтальпии водяного пара при его нагреве от температуры 373.15 до 2000 К. Укажем это новое значение температуры в ячейке А13.
Скопируйте ячейку С12 и вставьте копию в ячейку С13. Активизируйте ее и посмотрите полученную формулу:
[=C10*(($А13^(C$1+1)-$A12^(C$1+1))/(C$1+1))].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.