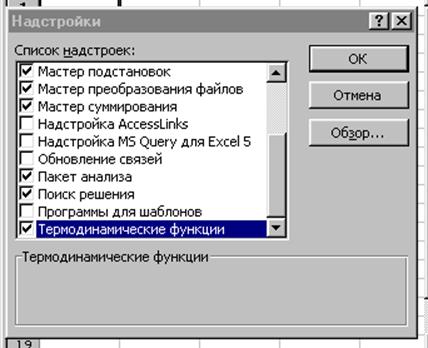
Рис. 13. Окно выбора доступных при работе надстроек
После этого в разделе «Определенные пользователем» появятся шесть известных специальных функций.
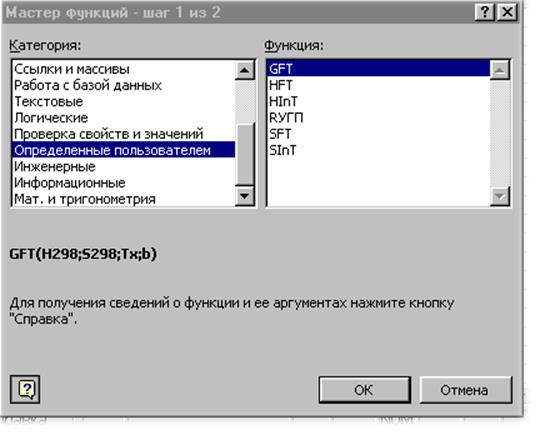
Рис. 14. Окно определенных пользователем функций со списком специальных функций для термодинамических расчетов
Дальнейшее их применение не отличается от описанного ранее, но теперь нет необходимости открывать какую-либо книгу вместе с рабочей.
Вычисления значений термодинамических свойств при заданной температуре являются основным вариантом расчета, в определенном смысле они могут называться прямыми и выполняются сравнительно просто. Существенно сложнее выполнить расчет температуры, при которой некоторое свойство примет заданное значение, но такие задачи тоже встречаются в практике термодинамических расчетов. Сложность здесь состоит в том, что аналитически обратная задача неразрешима, поскольку уравнение является трансцендентным.
Электронные таблицы содержат встроенные инструменты решения трансцендентных уравнений, которые и следует применять при решении рассматриваемых задач. Это сервисные функции (меню «Сервис») «Подбор параметра» и, более мощная, «Поиск решения». Последняя присутствует в меню, если в надстройках отмечено одноименное название (см. рис. 13).
Для иллюстрации возможностей обратных вычислений решим стандартную задачу такого типа – определим температуру, при которой константа равновесия реакции водяного газа
CO + H2O = CO2 + H2
равна единице.
Результаты поиска свойств реагентов в таблице Init поместим в ячейку А1, а в таблице Termo – в ячейку А7. Укажем произвольную температуру, например, 1000 К в ячейке Е2 и рассчитаем для нее константу равновесия реакции. Для этого в столбце F вычислим изменения стандартных энергий Гиббса для всех реагентов, используя следующие формулы:
F2 ® [=GFT(C2;D2;$E$2;C8:I8)];
F3 ® [=GFT(C3;D3;$E$2;C9:I9)];
F4 ® [=GFT(C4;D4;$E$2;C10:I10)];
F5 ® [=GFT(C5;D5;$E$2;C11:I12)].
Легко заметить, что для этого достаточно ввести формулу в ячейку F2, скопировать ее в ячейки F3–F5 и отредактировать формулу в ячейке F5, изменив последнюю цифру с учетом того, что вода превращается в пар.
В соседнем столбце (G) расставим стехиометрические множители реагентов и вычислим стандартное изменение энергии Гиббса в реакции водяного газа при указанной в ячейке Е2 температуре, введя в ячейку F6 формулу [=СУММПРОИЗВ(F2:F5;G2:G5)]. Это значение должно быть равно нулю, когда константа равновесия равна единице.
Вызовем сервис «Подбор параметра». В поле ввода «Установить в ячейке:» укажем ссылку на ячейку F6. В поле «Значение:» укажем «0», а в поле «Изменяя значения в ячейке:» укажем ссылку на ячейку Е2.
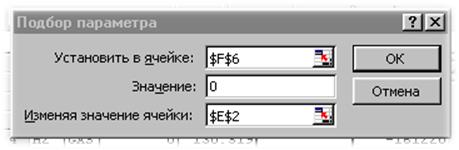
Рис. 15. Окно настройки сервиса «Подбор параметра»
Нажмем кнопку ОК и в ячейке Е2 получим искомый результат в абсолютной шкале температур. В соседней ячейке снизу (Е3) приведено то же значение в шкале Цельсия. Обратите внимание, что в результате работы сервиса «Подбор параметра» в ячейке действительно оказалось нулевое значение. Поскольку оно вычисляется независимо от каких-либо сервисов, его можно рассматривать как проверку корректности полученного решения.
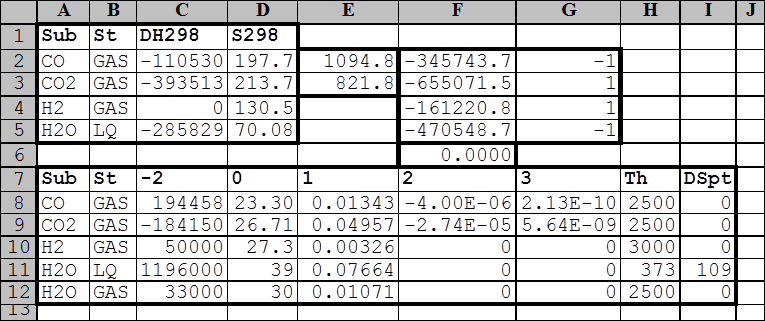
Рис. 16. Исходные данные и результаты расчета температуры, при которой константа равновесия реакции водяного газа равна единице
Полученное значение
отличается от приводимого в литературе примерно на 12 градусов, что, видимо,
характеризует точность термодинамической информации.
Список литературы
1. Краткий справочник физико-химических величин / Под. ред. А.А. Равделя и А.М. Пономарева. Л.: Химия, 1983. 232 с.
2. Казачков Е.А. Расчеты по теории металлургических процессов. М.: Металлургия, 1988. 288 с.
3. Владимиров Л.П. Термодинамические расчеты равновесий металлургических реакций. М.: Металлургия, 1970. 528 с.
4. Синярев Г.Б., Ватолин Н.А. и др. Применение ЭВМ для термодинамических расчетов металлургических процессов. М.: Наука, 1982. 263 с.
5. Григорян В.А., Стомахин А.Я. и др. Физико-химические расчеты электросталеплавильных процессов. М.: Металлургия, 1989. 288 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.