Расчет плоских ферм и арок. Расчетная схема фермы с принятой нумерацией узлов и стержней

Без вывода приводим для отдельного конечного элемента стержня фермы в общей системе координат матрицу жесткости |k|

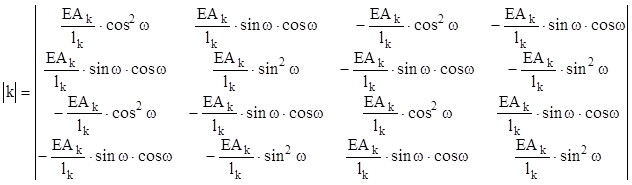,         (10)

матрицу неизвестных перемещений , а также матрицу узловых усилий

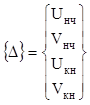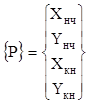,           .                                                         (11)

В выражениях (10, 11) приняты следующие обозначения:

E - модуль упругости;

A_k - площадь сечения стержня;

l_k - длина стержня;

 - угол наклона стержня к горизонтальной оси 0Х;

U - перемещения какого-либо узла вдоль оси 0Х;

V - перемещения какого-либо узла вдоль оси 0Y;

X - проекция внешней силы, приложенной к узлу, на ось 0X;

Y - проекция внешней силы, приложенной к узлу, на ось 0Y;

нч - индекс, указывает на начальный узел стержня в ЛСК (любой из двух узлов);

кн - индекс, указывает на конечный узел стержня в ЛСК (другой из двух узлов).

Подставляя в уравнение (6) выражения (10, 11) имеем СУ равновесия отдельного КЭ.

Так первое уравнение, записанное в развернутом виде

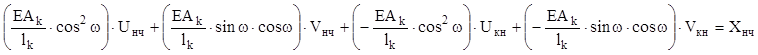
представляет собой уравнение равновесия для начального в ЛСК узла вдоль оси 0Х.

Второе уравнение

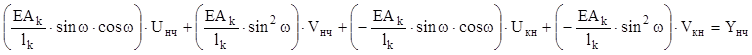
представляет собой уравнение равновесия для начального в ЛСК узла вдоль оси 0Y.

Третье уравнение

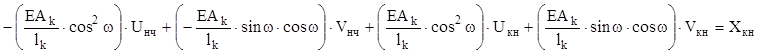
представляет собой уравнение равновесия для конечного в ЛСК узла вдоль оси 0Х.

И, наконец, четвертое уравнение

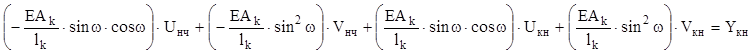
представляет собой уравнение равновесия для конечного в ЛСК узла вдоль оси 0Y.

Теперь ясно, каким образом угол поворота узлов не вызывает деформаций КЭ стержня фермы. Просто нет соответствующих уравнений равновесия относительно углов поворотов, вследствие чего повороты заведомо равны нулю.

Все, что Вам нужно знать для расчета плоских ферм по МКЭ - это выражения (9, 10) для отдельного стержня и знание правил составления глобальной матрицы жесткости для всей системы (этап 5 расчета по МКЭ), которые мы продемонстрируем на двух простых тестовых примерах. Определение деформаций и усилий (этап 6 расчета по МКЭ) также будет рассмотрен в тестовых примерах.

Поскольку в конце методического указания приведен код работающей программы по расчету ферм на языке С++, в котором индексация массивов начинается с нуля, то в тестовых примерах первый узел или стержень являются нулевыми по порядку перечисления, второй узел или стержень - первыми и т. д.

Тестовый пример № 1.

Расчетная схема фермы с принятой нумерацией узлов и стержней (числа в скобках) приведена на рис. 6. Отметим, что возможна любая другая нумерация. Общее количество узлов фермы - 3, стержней - 2. Опоры в узлах 0 и 2 - шарнирно неподвижные. Углы наклона стержня (0)  и стержня (1) . Более точные координаты узла 1: x = 50 см, y = 86.60254 см.

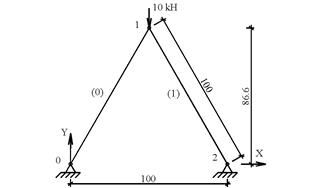
Рис. 6. Расчетная схема фермы тестового примера № 1.

Выбранные единицы измерений - kH и см.

Все стержни имеют одинаковые характеристики: Е = 2.06^.10⁴ kH/см², А_k = 10 см², l_k = 100 см.

Определяем коэффициенты матрицы жесткости стержня (0).

Вынесем за пределы знака матрицы множитель 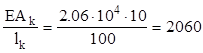 и запишем матрицу жесткости стержня (0), соединяющего узлы 0 и 1

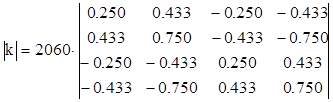                              .  (12)

Матрицу  мысленно можно разбить на четыре блока (показано пунктиром в выражении 12), каждый размером 2х2 коэффициентов. Это мысленное разбиение потребуется чуть позже при составлении глобальной матрицы жесткости фермы.

Определяем коэффициенты матрицы жесткости стержня (1).

Вынесем за пределы знака матрицы множитель 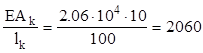 и запишем матрицу жесткости стержня (1), соединяющего узлы 1 и 2

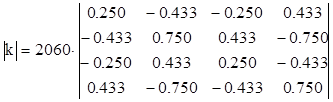                              .  (13)

Матрицу стержня (1) также мысленно разобьем на четыре блока.

Теперь составим глобальную матрицу жесткости фермы. Общее число узлов фермы равно трем. Число линейных перемещений (угловые отсутствуют) трех узлов в ЛСК для плоской фермы равно числу узлов, то есть тоже трем. Каждое линейное перемещение раскладывается в ГСК на две проекции вдоль координатных осей, то есть число неизвестных перемещений, подлежащих определению, равно 3^.2=6. Поэтому создаем глобальную матрицу жесткости фермы размером 6х6, заполненную нулями

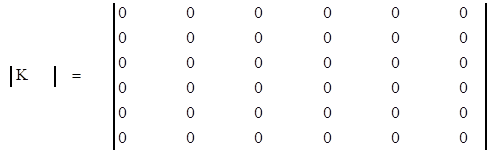
Глобальную матрицу жесткости тоже мысленно разобьем на блоки размером 2х2 коэффициентов.

Заполним (точнее просуммируем по определенному правилу) матрицу  матрицей  стержня (0). Как следует из рассмотрения выражения (12) и поясняющих надписей к нему левый верхний блок матрицы  стержня (0) (см. рис. 7 а) должен располагаться на пересечении коэффициентов нулевого узла в строке глобальной матрицы  (по горизонтали) и опять же нулевого узла в столбце глобальной матрицы  (по вертикали). На рис. 7 темным цветом обозначен тот блок, который заполняет блок глобальной матрицы с указанными на рисунке индексами (первые индексы - номера блоков в строке глобальной матрицы жесткости, вторые - номера блоков в столбце той же матрицы). Так левый верхний блок матрицы жесткости стержня (0) заполняет (как отмечено чуть выше) блок глобальной матрицы в нулевой строке и нулевом столбце. Левый нижний - блок глобальной матрицы в первой строке и нулевом столбце и так далее. Правый верхний - блок глобальной матрицы в нулевой строке и первом столбце. Правый нижний - блок глобальной матрицы в первой строке и первом столбце. После определения положения блока матрицы  в матрице , коэффициенты блока первой матрицы складываются с коэффициентами соответствующего блока последней. И так для всех блоков.