|
0, 0 |
1, 0 |
0, 1 |
1, 1 |
Рис. 7. К заполнению глобальной матрицы жесткости. Блоки матрицы |k| стержня (0):
а) левый верхний; б) левый нижний; в) правый верхний; г) правый нижний.
Аналогичный подход применяется к определению местоположения блоков матриц отдельных стержней в глобальной матрице жесткости фермы для каждого стержня. Для стержня (1) индексы расстановки блоков матрицы |k| в глобальной матрице |K| будут
|
|
1, 1 |
1, 2 |
. |
|
2, 1 |
2, 2 |
При первом сложении матрицы ![]() с матрицей
с матрицей ![]() стержня
(0) с учетом правила расположения блоков матрицы жесткости отдельного стержня
получим
стержня
(0) с учетом правила расположения блоков матрицы жесткости отдельного стержня
получим
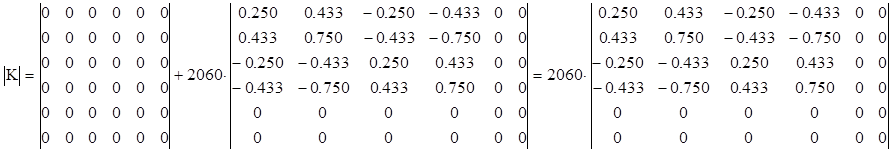
При
втором сложении матрицы ![]() с матрицей
с матрицей ![]() стержня (1) получим
стержня (1) получим
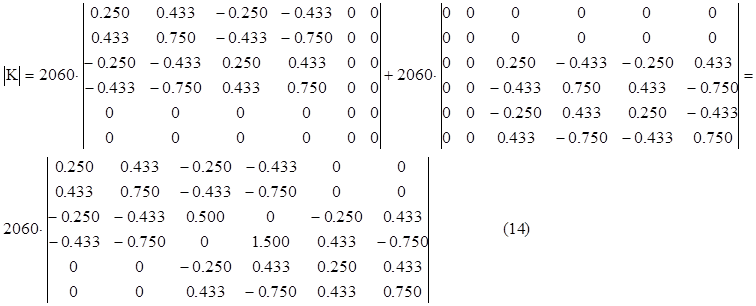
Матрица-столбец неизвестных перемещений выглядит как последовательное перечисление перемещений вдоль осей 0Х и 0Y каждого узла фермы
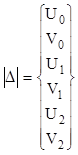 .
.
Из внешних нагрузок в первом тестовом примере приложена только одна к узлу 1 против оси 0Y. По всем другим направлениям и в других узлах внешние силы равны нулю. Матрица-столбец внешних сил выглядит как последовательное перечисление сил вдоль осей 0Х и 0Y каждого узла фермы
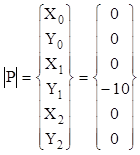 .
.
Перепишем систему уравнений для определения перемещений узлов фермы в виде (1)
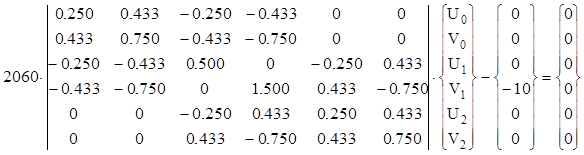 . (15)
. (15)
Заметим, что перемещение вдоль оси 0Х узла 0 равно нулю, так как по этому направлению в этом узле установлена линейная связь. А это означает, что соответствующие строка (уравнение равновесия нулевого узла вдоль оси 0Х - нулевая строка в глобальной матрице жесткости, матрице неизвестных перемещений и матрице внешних сил) и столбец (коэффициенты уравнения равновесия нулевого узла вдоль оси 0Х - нулевой столбец в матрице жесткости) можно вычеркнуть. Этим мы и учтем рассматриваемую внешнюю связь, и сократим порядок решаемой системы уравнений, что приведет к экономии времени вычислений. По такому же принципу учтем наличие внешних связей вычеркиванием из СУ (15) вместе с нулевой строкой и столбцом еще строки и столбцы с номерами 1, 4, 5. Так как индексация принята с нуля, то строка 5 - последняя по номеру.
Окончательная система уравнений выглядит как
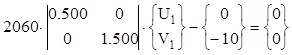 .
.
Решение этой системы уравнений: U1 = 0, V1 = -0.0032 см. Знак минус означает, что перемещение узла 1 произойдет вниз против оси 0Y.
При деформировании фермы координаты узла 1 изменились: координата x - 50 см, y - 86.5993 см.
При определении деформаций стержня будет пользоваться следующей последовательностью действий (соответствует расчету ферм по недеформированной схеме; подобный алгоритм определения деформаций используется в SCAD):
- по координатам узлов стержня после деформирования фермы определяем его новую длину (рис. 8)
lk новая = ![]() ,
,
где xнч, yнч - координаты начального узла (любой из двух) фермы после ее деформирования;
xкн, yкн - координаты конечного узла (отличный от начального) фермы после ее деформирования;
- определяем новый угол наклона стержня также по координатам его узлов
![]() ;
;
- определяем разность углов наклона по модулю нового положения стержня и первоначального (угол отклонения)
![]() ;
;
- находим проекцию новой длины стержня
![]() ;
;
- деформация стержня (отрицательная деформация - сжатие, положительная - растяжение)
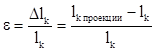 .
.
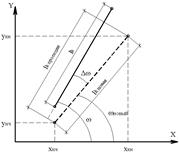
Рис. 8. К определению деформаций стержня.
Первоначальная
длина стержня (0) равна 100 см, а из решения прямоугольного треугольника новая
длина -![]() см. Угол отклонения от первоначального
положения (до деформирования фермы)
см. Угол отклонения от первоначального
положения (до деформирования фермы) ![]() рад. Проекция новой
длины - 99.9971971 см. Деформация
рад. Проекция новой
длины - 99.9971971 см. Деформация 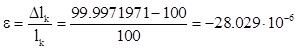 . Усилие в стержне
сжимающее
. Усилие в стержне
сжимающее ![]() kH. Такое же усилие по величине и
по знаку возникает в стержне (1).
kH. Такое же усилие по величине и
по знаку возникает в стержне (1).
Тестовый пример №2.
Потренируемся еще, взяв исходные данные из примера № 1, добавив горизонтальный стержень (2) с теми же характеристиками (рис. 9) и убрав внешнюю связь в узле 2 по направлению оси 0Х (шарнирная ферма). Внешнюю нагрузку оставим без изменения.
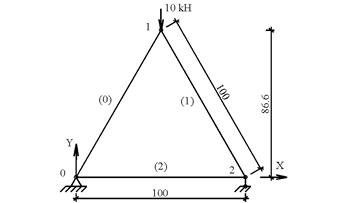
Рис. 9. Расчетная схема фермы тестового примера № 2.
Находим матрицу жесткости стержня (2).
![]()
Также вынесем за пределы
знака матрицы множитель 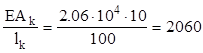 и запишем матрицу
жесткости стержня (2)
и запишем матрицу
жесткости стержня (2)
|
коэффициенты 0-го узла |
коэффициенты 2-го узла |
![]()
![]()
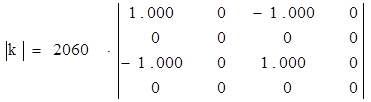 .
.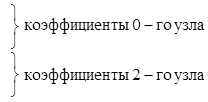 (16)
(16)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.