Разработка вариантов мостового перехода висячей системы, страница 13

 ║     │     │         │         │         │         │         │         ║

 ║     │     │         │         │         │         │         │         ║

 ╚═════╧═════╧═════════╧═════════╧═════════╧═════════╧═════════╧═════════╝

4.2 Расчет балки жесткости

Построим огибающие изгибающего момента и продольной силы в балке жесткости.

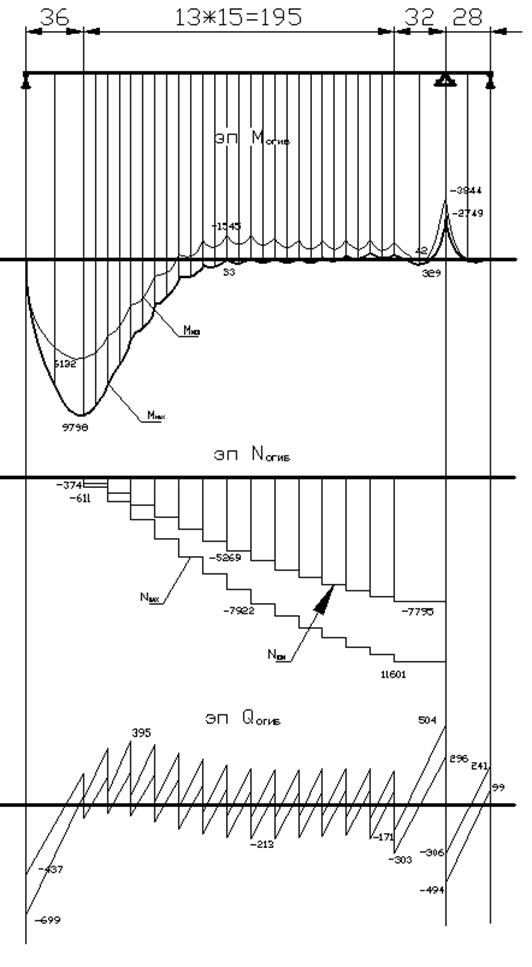
рис. 5 Эпюры усилий в балке жесткости

4.2.1 Определение характеристик сечения балки и

проверка по напряжениям

          Руководствуясь нормами и типовыми проектами, назначим размеры  и материал сечения.

          Выберем коробчатое пролетное строение, изготавливаемое из мостовой стали 15ХСНД с расчетным сопротивлением – R_Y= 3*10⁴ т/м².

          Сечение пролетного строения с ортотропной плитой показано на листе №2 чертежей. Для расчета оно приводится к Н-образному сечению, показанному на рисунке 5.

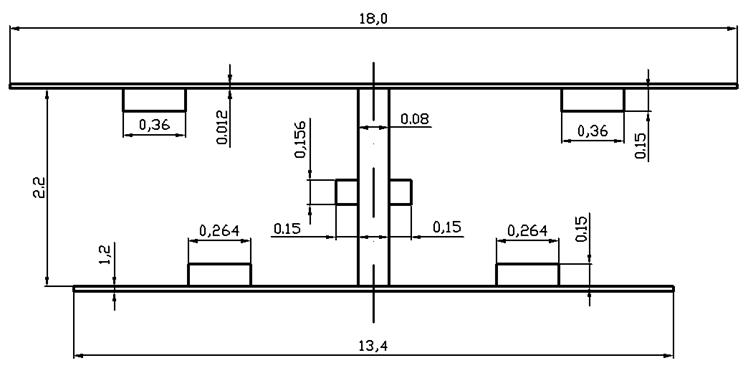
Рис. 6 Расчетное сечение балки жесткости

Некоторые параметры подобраны при расчете проезжей части: толщина покрывающего листа и стрингеров – 12мм, расстояние между продольными ребрами – 30см, их высота -15см.

          Назначим высоту стенки балки толщиной 20мм – 2,25м, ширина нижнего пояса балки – 13,4м при толщине –12мм.

          Далее, с помощью программы «Geometr» рассчитаем площадь и момент сопротивления выбранного сечения.

  ПРОГРАММА "ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ"

  Название объекта: Металл

  Матеpиал констpукции: металл

  Число элементов металлического сечения: 9

  Cостав сечения (измеритель - м):

 ╔═════════╤═════════╤═════════╤═════════╤═════════╤═════════╤═════════╗

 ║   N/N   │Горизонт.│Вертикал.│Координ. │Координ. │   Тип   │Угол beta║

 ║элементов│размер-a │размер-h │ц.т. - x │ц.т. - y │элемента │  град.  ║

 ╚═════════╧═════════╧═════════╧═════════╧═════════╧═════════╧═════════╝

      1      18.000    0.012     0.000     0.000       1       0.000

      2      13.400    0.012     0.000    -2.212       1       0.000

      3      0.080     2.200     0.000    -1.106       1       0.000

      4      0.360     0.150    -4.500    -0.080       1       0.000

      5      0.360     0.150     4.500    -0.080       1       0.000

      6      0.264     0.150    -3.350    -2.131       1       0.000

      7      0.264     0.150     3.350    -2.131       1       0.000

      8      0.150     0.156    -0.075    -1.106       1       0.000

      9      0.150     0.156     0.075    -1.106       1       0.000

  Геометрические характеристики сечения:

  F=  7.8680000000E-01 кв.м

  xc=  0.0000000000E+00 м 

  yc= -9.9074936451E-01 м

  Ix=  6.1880009604E-01 м⁴ 

  Iy=  1.1315997260E+01 м⁴

  Ixy=  0.0000000000E+00 м⁴ 

  Ik=  2.1485530667E-03 м⁴

  rx=  9.5581069913E-01 м

  ry=  3.7924009020E+00 м

  Imax= 1.1315997260E+01 м⁴ 

  Imin= 7.1880009605E-01 м⁴

  alfa=  0.0000000000E+00 рад.

  Wxv= 7.2114427321E-01 м³

  Wxn= 5.8569951016E-01 м³

  Wyp= 1.2573330289E+00 м³ 

  Wyl= 1.2573330289E+00 м³

  Wk= 1.4323687111E-02 м³

  Sx= 6.5115204654E-01 м³

  Sy= 1.1345150000E+00 м³

  xu=  3.1632393581E-13 м 

  yu=  8.6499344638E-02 м

  Iom= 1.2284420247E+01 м⁶

4.2.2 Расчет на прочность

Проверка по нормальным напряжениям ведется из условия:

,

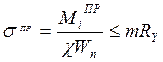где

          M_i^ПР – расчетный изгибающий момент в данном сечении при расчете на

прочность;

          χ=1,05 – коэффициент учета ограниченного развития пластических

деформаций;

          W_n – момент сопротивления сечения нетто;

          m= 0,9 – коэффициент условий работы;

          R_Y – расчетное сопротивление материала.

Проверка по касательным напряжениям ведется из условия:

,

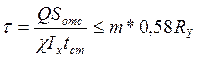где

          Q – расчетная поперечная сила;

          S – статический момент сдвигаемой части сечения брутто;

          χ=1,05 – коэффициент, учитывающий неравномерность распределения

напряжений;

          I_x – момент инерции сечения брутто;

          t_ст  - толщина стенки;

Проверим балку в двух сечениях: по максимуму изгибающего момента и поперечной силы.

1. по нормальным напряжениям (узел №2, х=36м):