Нелинейные колебания и устойчивость фермы мизеса

Кафедра «Прочность материалов и конструкций»

Лабораторная работа №2

НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ И УСТОЙЧИВОСТЬ ФЕРМЫ МИЗЕСА

Выполнил:                                                                       Студент группы ТМ-503

            Егоров Г.Д.

Принял:                                                                                               Рыбина И.И.

Санкт-Петербург

2009

Исходные данные:

.

.

Номер узла	Координаты узла
	X	Y
1	0	-8
2	-6	0
3	6	0

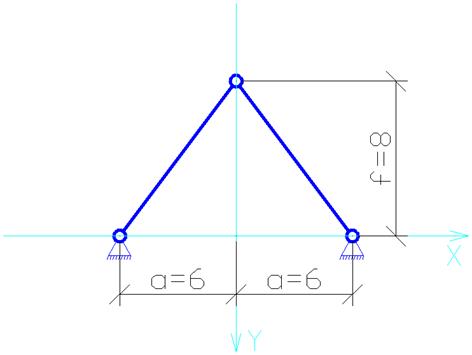
Исследование ведётся в специально разработанной программе с помощью особого графика – фазовой диаграммы, на которой изображены в осях вертикальная и горизонтальные скорости.

1. Положения равновесия

;

;

;

;

.

А.

Номер узла	Координаты узла
	X	Y
1	0	-8
2	-6	0
3	6	0

Б.

Номер узла	Координаты узла
	X	Y
1	0	0
2	-6	0
3	6	0

В.

Номер узла	Координаты узла
	X	Y
1	0	8
2	-6	0
3	6	0

Г.

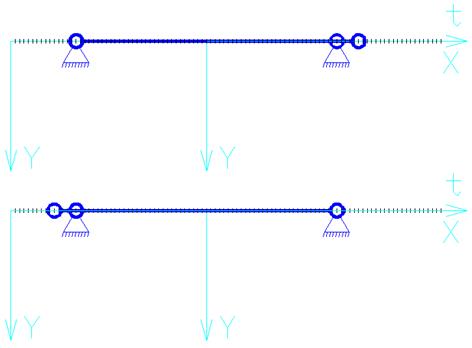
2. Задаем смещение верхнего шарнира вдоль оси Y и задаем начальную скорость по этой же оси.

;

;

 - изменяем;

;

.

А. Смещаем шарнир на одну единицу вверх (Y = -9)

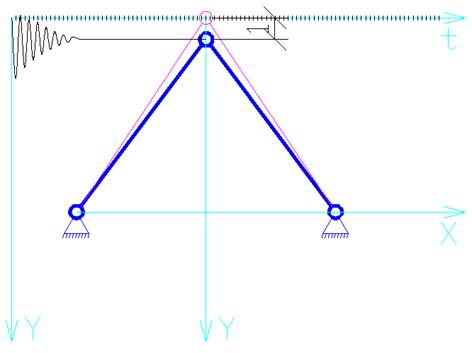
Максимальное смещение по оси Y составило  (от начала координат).

Система находится в устойчивом состоянии равновесия.

Б. Смещаем шарнир на 17 единиц вниз (Y = 9)

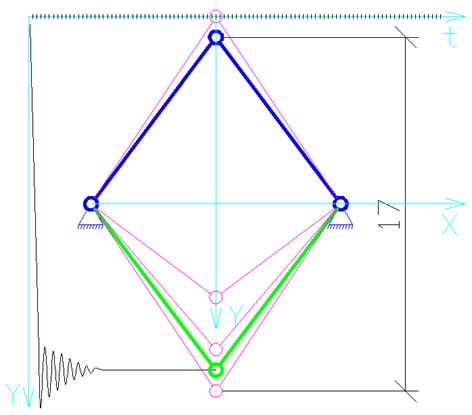
Максимальное смещение по оси Y составило  (от начала координат).

Система потеряла устойчивость и перешла в другую форму равновесия.

3. Задаем смещение верхнего шарнира вдоль оси Х и задаем начальную скорость по оси Y.

;

 - изменяем;

;

;

.

Смещаем шарнир на 7 единиц влево (Х = -7)

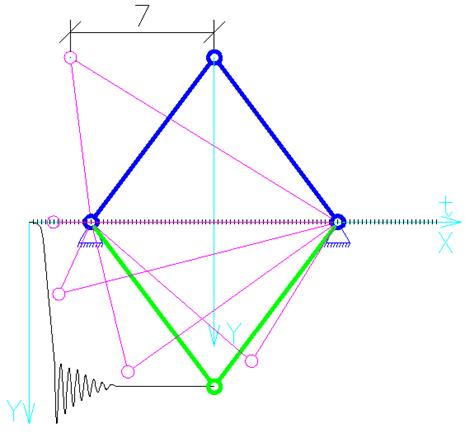
Максимальное смещение по оси Y составило  (от начала координат).

Система перешла в другую форму равновесия.

4. Находим значение вертикальной критической силы.

Задаем нагрузку вдоль оси Y.

 - изменяем;

;

;

;

.

А. .

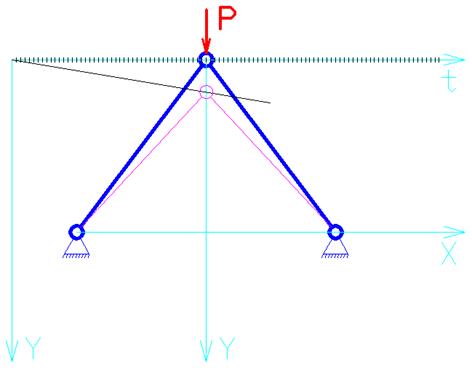
Система устойчивость не потеряла, следовательно .

Б. .

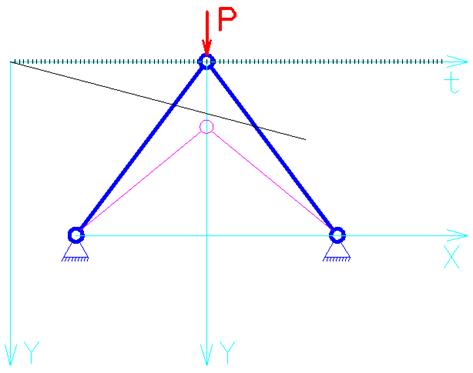
Система устойчивость не потеряла, следовательно .

В. .

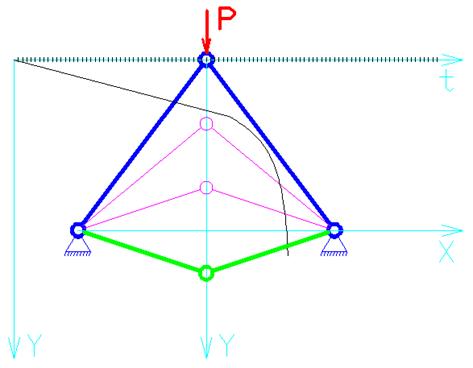
Система потеряла устойчивость и перешла в смежную форму равновесия.

Таким образом, .

5. Исследуем систему на устойчивость при совместном действии вертикальной сосредоточенной силы и горизонтального смещения шарнира.

;

;

;

;

.

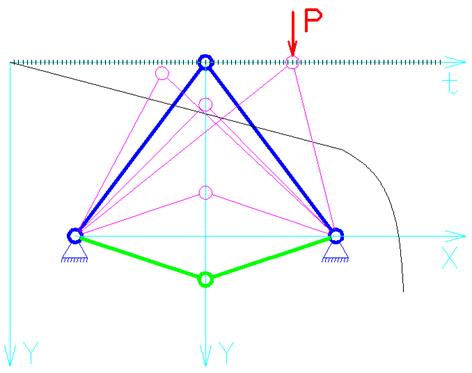
В следствии начального смещения шарнира по горизонтали произошли затухающие колебания. Система потеряла устойчивость и перешла в смежную форму равновесия.

Таким образом, .

6. Определяем высоту фермы при которой будет теряться устойчивость при том же пролете и том же значении критической силы.

Задаем различные значения высоты фермы.

Задаем начальное горизонтальное смещение шарнира

Ферма теряет устойчивость и переходит в смежную форму равновесия при высоте 25.

(Y = -25)

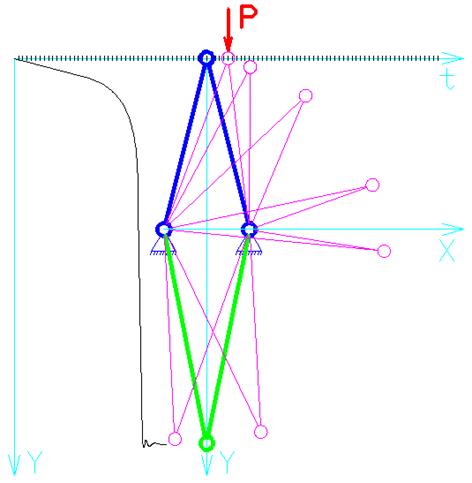
Максимальное смещение по оси Y составило  (от начала координат).

.

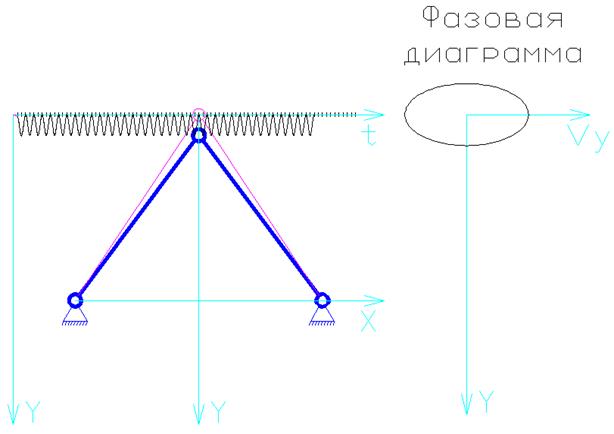
7. Считаем, что центральный узел несет в себе сосредоточенную массу.

Задаем смещение верхнего шарнира по вертикали при нулевой вязкости.

.

А. Смещаем шарнир на одну единицу вверх (Y = -9)

Б. Смещаем шарнир на три единицы вверх (Y = -11)

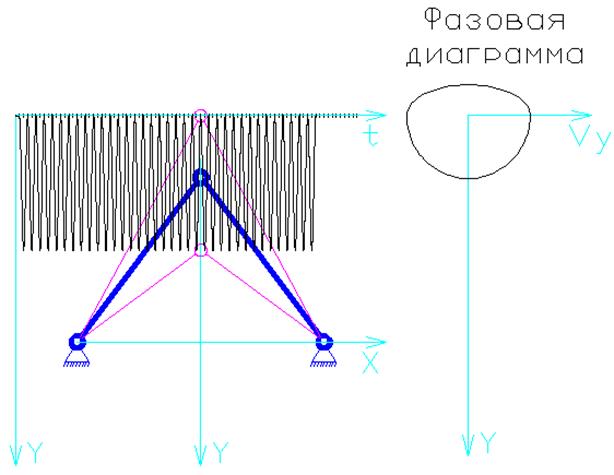
Путем наблюдений было установлено, что система теряет устойчивость при смещении верхнего шарнира вверх на 4,65 (Y = -12.65). При этом происходят свободные гармонические колебания.

В. Смещаем шарнир на пять единиц вверх (Y = -13)

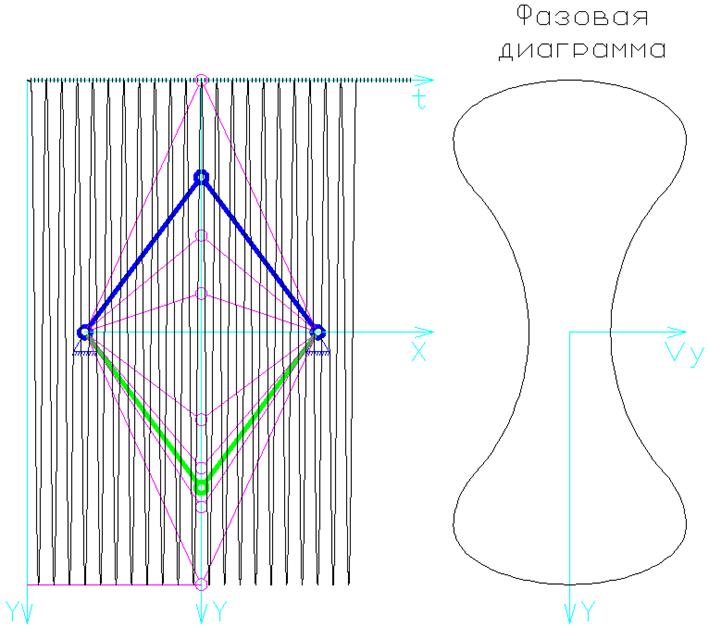
Скелетная кривая – график, отражающий зависимость условной частоты от условной амплитуды.

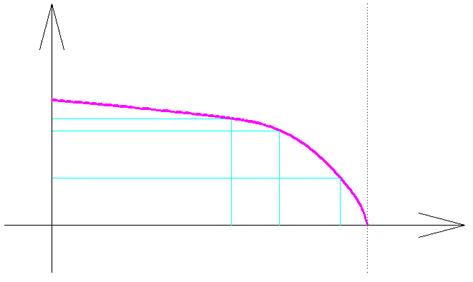
8. При заданном смещении верхнего шарнира по вертикали изменяем значение вязкости.

Смещаем верхний шарнир на 7 единиц вверх (Y = -15)

.

А. .

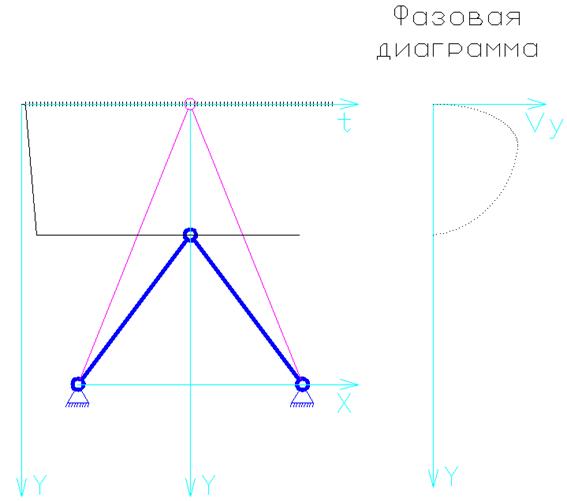
Б. Уменьшаем вязкость: .

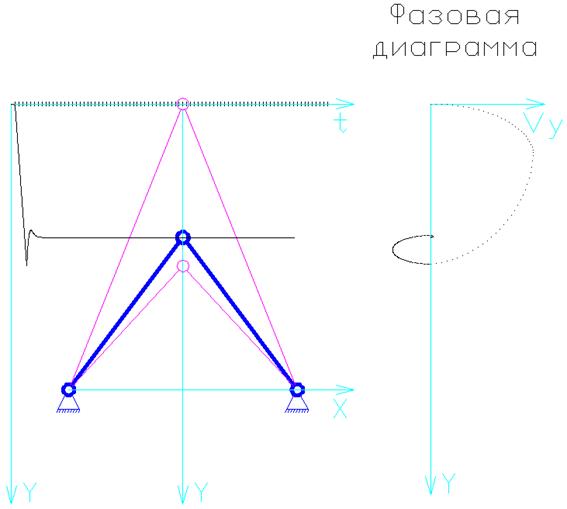
В. Уменьшаем вязкость: .

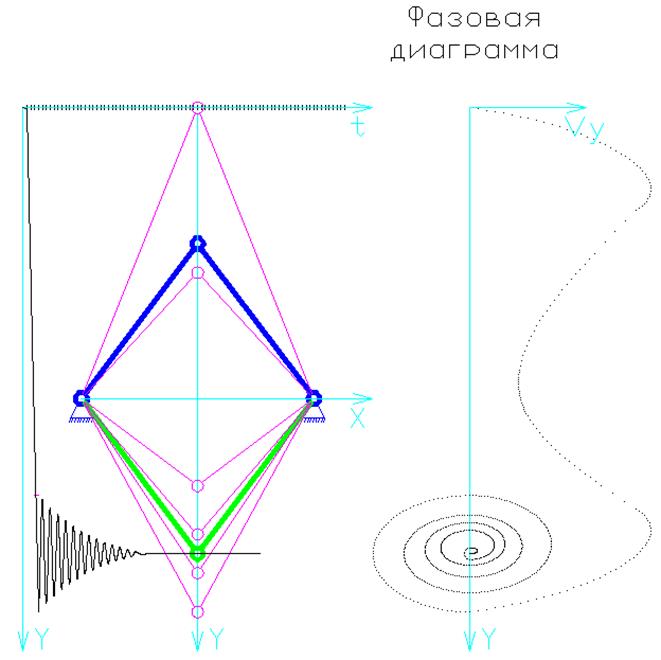
Система потеряла устойчивость и перешла в смежное состояние равновесия. При этом происходят затухающие колебания.