2.1. Приближённое решение волнового уравнения для атома с двумя электронами.
При точной записи и решении волнового уравнения для атомов и молекул необходимо учитывать не только движение электронов, но и ядер. Однако, как показывают расчёты, из-за их огромной массы по отношению к массе электронов, движение ядер можно не учитывать. Такой подход называется адиабатическим приближением или приближением Борна-Оппенгеймера. Далее и всегда мы будем рассматривать уравнение Шредингера для системы, состоящей только из электронов.
Движение одного электрона в потенциальном поле (V) описывается следующим волновым уравнением:
.
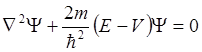(2.1)
Для описания более сложных атомов необходимо обобщить уравнение 2.1 так, чтобы оно описывало состояние двух и более электронов. Новое уравнение должно учитывать взаимодействие электронов с ядром и между собой, а также независимость друг от друга положения электронов. В случае двух электронов новая волновая функция будет зависеть от координат обоих электронов Y(x1,y1,z1, x2,y2,z2). Потенциальная энергия системы будет суммой потенциальных энергий каждого электрона по отношению к ядру и энергией их взаимодействия между собой: V = V1(x1,y1,z1) + V2(x2,y2,z2) + V12. V1 и V2 выражаются аналогичными функциями V1 = eZe/r1 и V2 = eZe/r2, а V12 = e2/ r12 (энергия взаимного отталкивания электронов) будет зависеть от расстояния между электронами (r12).
Таким образом волновое уравнение для двух электронов можно записать в следующем виде:
Ñ12Y + Ñ22Y + 
(E - V1 - V2
-
)Y =
0. (2.2)
Y2(x1,y1,z1, x2,y2,z2) - вероятность найти электрон № 1 в точке (x1,y1,z1) и электрон № 2 в точке (x2,y2,z2).
Точное решение уравнения 2.2 получить нельзя, т.к. в
него входит неопределенная переменная r12. Для решения
уравнения можно пренебречь переменной . В
этом случае каждый электрон будет находиться на определенных уровнях независимо
от того, какой уровень занимает другой электрон. Если электроны занимают уровни
1 и 2, то полная энергия системы Е = Е1
+ Е2. Такое значение мы получим, решая ур.2.2.
Решение уравнения 2.2 будем искать в виде сложной волновой функции
(2.3)
или для упрощения записи Y = Y(1) ×Y(2), где Y(1) = Y(x1;y1;z1) зависит только от координат первого электрона, а Y(2) – только от координат второго электрона. Ñ12 действует только на Y(1), а Ñ22 - на Y(2).
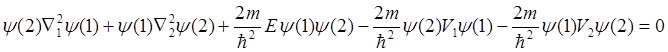(2.4)
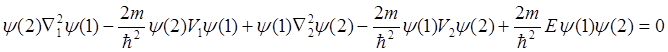(2.4*)
Состояние системы с электроном с № 1 будет удовлетворять уравнению:
;
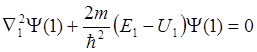(2.5)
или
.
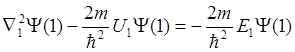(2.5*)
Соответственно и для электрона № 2:
;
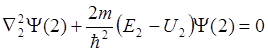(2.6)
или
.
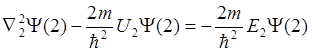(2.6*)
Заменяя левые выражения из ур.2.4* на соответствующие правые выражения из ур.2.5* и 2.6*, получим Е = Е1 + Е2.
Т.о. при отсутствии взаимодействия между электронами (V12 = 0) произведение двух волновых функций для одного электрона Y = Y(1) ×Y(2) будет решением волнового уравнения для двух электронов, а энергия всей системы представляет собой сумму энергий каждого отдельного электрона. Однако следует заметить, что
1. Точное решение было получено благодаря пренебрежению взаимодействием электронов.
2. Использованная волновая функция не является функцией в 3-мерном пространстве. Функция Y(x1,y1,z1, x2,y2,z2) может быть представлена только в 6-мерном пространстве (в общем случае для n электронов в 3n-мерном пространстве). Это обстоятельство еще раз указывает на то, что Y не отражает какие-либо реальные характеристики электрона, а служит лишь для описания движения двух электронов. Функция в пространстве шести измерений не может быть исследована экспериментально.
2.2 Обменное вырождение.
Решение 2.3 волнового уравнения 2.2 без учета взаимодействия между электронами описывает такое состояние системы, при котором один электрон находится в состоянии 1, а другой в состоянии 2. Решение 2.3 не единственное. Из-за неразличимости электронов № 1 и № 2 решением ур.2.2 будет и функция:
.
(2.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.