Волновое уравнение для двух электронов. Методы решения волнового уравнения, страница 5

 Т.к. волновое уравнение при учете взаимодействия между электронами не решается точно, то будем искать приближенное решение. Наличие потенциала взаимодействия V₁₂ приводит к взаимному искажению орбит электронов. Приближение будет заключаться в том, что мы не будем учитывать влияние одного электрона на вид орбиты другого электрона. Другими словами мы будем оперировать невозмущенными волновыми функциями электронов. Поэтому в нашем случае, при использовании оператора возмущения V₁₂ = 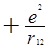и l = 1, нам надо решить уравнение

          .

Так как , то получим:

          .

Отсюда средняя энергия возмущения определяется следующим выражением:

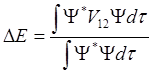          ,                                                                                  (4.7)

Величина DЕ дает первое приближение изменения энергии всей системы, вызванного потенциалом взаимодействия между электронами V₁₂. В общем случае, когда коэффициент l не известен, в соответствии с теорией возмущения Релея-Шрёдингера величины Y и E раскладывают в степенные ряды, составляют и решают совместно уравнения с необходимой степенью порядка, находя соответствующие поправки.

          В качестве примера вычислим энергию возмущения DЕ для атома Не.  Для расчётов возьмём невозмущенную волновую функцию

          .                                                                   (4.8)

Подставив 4.8 в 4.7, получим:

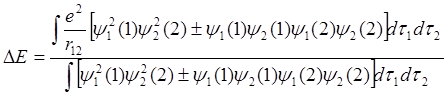.                               (4.9)

Подставляя в 4.9 волновую функцию в явном виде, можно вычислить значение DЕ. Рассмотрим выражение 4.9 подробнее. Обозначим первый интеграл в числителе буквой С.

С =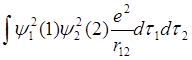                                                                   (4.10)

Произведения еY₁²(1) и еY₂²(2) можно назвать плотностью заряда. Здесь мы имеем “размазанный” заряд или зарядовое облако. Эти зарядовые облака отталкиваются друг от друга согласно закону Кулона. Интеграл С представляет собой энергию такого взаимодействия. Второй член в числителе выражения 4.9 обозначим буквой А.

A= 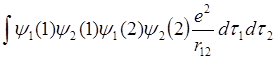                             (4.11)

Данный интеграл свидетельствует о том, что электроны тождественны и могут обмениваться местами. Или можно сказать, что электрон 1 частично находится в состоянии № 1, а частично в состоянии № 2 - [Y₁(1)Y₂(1)]. То же относится и к электрону 2. Интеграл А следует толковать как взаимодействие между собой различных частей одного размазанного заряда. Плотности этих зарядов [еY₁(1)Y₂(1)] и [еY₁(2)Y₂(2)]. Фактически это обменная плотность заряда, а величина А - обменная энергия.

          Появление обменной энергии +А и -А (и обменного заряда) типично для квантовой механики и является результатом неразличимости двух электронов № 1 и № 2 и использованием для описания их поведения волновых функций. Наличие обменной энергии  А важно для объяснения атомных спектров и понимания химической связи (а именно, гомеополярной связи).

          Если волновые функции нормированы, тогда:

.                                                            (4.12)

Кроме того, согласно теореме об ортогональности (об этом будет сказано ниже):

.                                                                      (4.13)

Поэтому второй интеграл в знаменателе выражения 4.9 при y₁ ¹ y₂ равен нулю, а сам знаменатель равен 1 и при y₁ = y₂ (1 = 2), либо равен 2, либо нулю. Можно показать, что C и A положительны (энергия отталкивания положительна).

Тогда для основного состояния (y₁ = y₂ и знак + в уравнении 4.9) получаем:

DЕ = C,                                                                                                (4.14)

(при знаке минус в уравнении 4.9 DЕ = 0). В этом состоянии электроны спарены и мы имеем синглет.

          При y₁ ¹ y₂ один из электронов находится в возбуждённом состоянии (ближайший уровень 2s) и мы имеем триплет, которому соответствуют два уровня:

          DE = C ± A.                                                                                          (4.15)

Графически данный результат представлен на рис 4.1.      

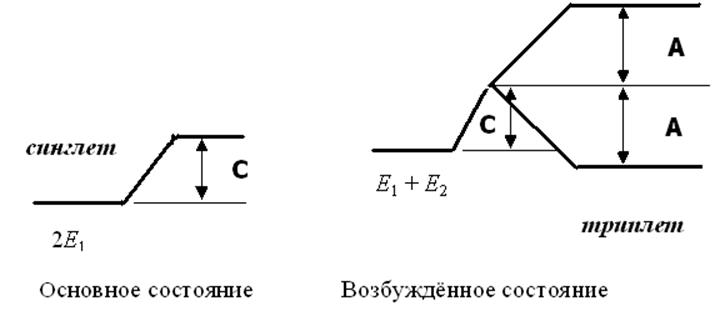
Рис. 4.1. Энергия возмущения для атома Не.