Волновое уравнение для двух электронов. Методы решения волнового уравнения, страница 4

Волновое уравнение Шредингера точно решается только для одноэлектронных систем, например, для атома водорода. Задачи для систем с двумя и большим числом электронов решаются при помощи приближённых методов. Следует отметить, что в большинстве случаев точные решения и не нужны. Чаще всего степень устойчивости молекул, направления и скорости химических реакций достаточно знать лишь в определённом интервале изменений параметров системы. В квантовой химии при расчётах наиболее распространёнными методами являются вариационный метод и теория возмущений.

4.1 Вариационный метод.

В квантовой механике постулируется, что если производить измерения какой-либо динамической переменной L системы, описываемой волновой функцией Y, то на основании этих результатов можно определить её среднюю величину.  При этом эта величина всегда будет выше истинного собственного значения L₀ оператора . Данное утверждение записывается в виде:

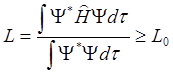.                                                                            (4.1)

В вариационном методе изменениям (вариациям) подвергается главным образом волновая функция, а гамильтониан может вообще оставаться без изменений. Обычно для расчётов используют линейный вариационный метод, называемый также методом Релея-Ритца. В этом случае искомая вариационная волновая функция Y выражается в виде линейной комбинации независимых функций со своими коэффициентами. Затем варьируются коэффициенты этой комбинации так, чтобы получить минимальную энергию.

Пусть волновая функция будет линейной комбинацией из n функций y_i:

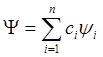,                                                                                           (4.2)

где c_i – вариационные параметры. Для вариационного метода уравнение 4.1 записывается в виде

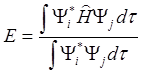                                                                                                (4.3)

Вводя обозначения  и  иподставляя выражение 4.2 в 4.3, получим

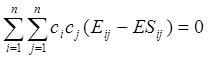          .                                                                        (4.4)

          Используя приём минимизации, т.е. дифференцируя 4.4 по c_k, получим систему так называемых секулярных или вековых уравнений:

          .

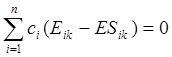Таким образом мы получаем n уравнений с n неизвестными (c_i). Такая система уравнений совместима только в том случае, если определитель, составленный из её коэффициентов, равен нулю

          ½Е_ik- ES_ik½ = 0.                                                                                  (4.5)

Определитель 4.5 называют вековым определителем. Все n корней (значений Е), получаемых при решении системы уравнений, соответствуют точкам стационарности интеграла 4.3. Наименьший корень даёт наилучшее значение энергии основного состояния.

4.2. Принцип теории возмущений.

Теория возмущений  сводит рассматриваемую задачу к задаче, отвечающей более простому случаю, когда искомые значения E_i, Y_i выражаются через известные значения E_o, Y_o, но с некоторым возмущением, т.е. изменением гамильтониана. Следует отметить, что в теории возмущений хорошие результаты получаются только тогда, когда применяемый гамильтониан  не сильно отличается от истинного гамильтониана рассматриваемой системы :

          ,

где  – возмущение. Значение параметра l находится в пределах 0 ¸ 1.

          Как мы уже установили ранее, если пренебречь взаимодействием электронов (V₁₂ = 0), то энергия атома равна сумме энергий двух электронов в состояниях 1 и 2:

Е = Е₁ + Е₂.                                                                               

Теперь рассмотрим, как изменится эта энергия при учете взаимодействия между электронами. Как известно потенциал кулоновского взаимодействия таков:

V₁₂ =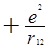.                                                                                        (4.6)