Экзаменационные билеты № 1-21 по дисциплине "Математика" (Уравнения и неравенства 1-ой степени. Преобразование тригонометрических функций в "х")

Билет №2

УРАВНЕНИЯ И НЕРАВЕНСТВА 1-ОЙ СТЕПЕНИ.

уравнение вида

ax² + bx +c=0   где a, b, c Є R, a ≠0 Называется квадратным уравнением. Они бывают полными и не полными.

1. c=0                               2.b=0  ax²+c=0 /a                                                   3.   b>c=0

ax²+bx=0                            x²+c/a=0                                                                      ax²=0

X (ax+b) =0                         Если c/a>0 то ур-ие не имеет                                    x=0.

a=0  x₂=-b/a                         корней т. к. Сумма неотрицательного

                                             и положительных чисел ≠0.

                                             Если c/a<0, то Ур-ие имеет 2 корня.

                                              X₁,x₂ ± √-c/a.

Теория 1

Если кв. уравнение ax²+bx+c=0 имеет действительные корни х₁ и х₂, то они вычисляются по формуле:

Х_1,2= -b±√Д/2a

1)  если Д=0, то уравнение имеет 2 корня (одинаковых) х₁= х₂ = х = -b/2a

2)  если Д<0, то уравнение не имеет действительных корней

3)  если Д>0, то уравнение имеет 2 действительных корня.

Теория 2

Если кв. уравнение ax²+bx+c=0 имеет действительные корни, то х₁+х₂= - b/2a

X1-x₂= -b/a         теорема Виета

    x₁· x₂= c/a

Т. Виета устанавливает зависимость между корнем и коэффициентом кв. уравнения.

Теорема 3

        Если квадратный трёхчлен ax²+bx+c имеет действительные корни х_{1 и}  х_2, то они могут быть представлены в виде произведения следующим образом:

ax² +bx+c = a(x-x₁) (x-x₂)

Билет №3

ОПРЕЛИТЕЛЬ 2 ПОРЯДКА. СИСТЕМА ДВУХ ЛЕНЕЙНЫХ УРАВНЕНИЙ.

Определителем 2-го порядка называется число, определённое неравенством:

∆= a₁ b₁ = a₁b₂ – a₂b₁

        a₂ b₂

числа а₁ и b₁, a₂  и b₂ называются элементами определителя, причём элементы a_1, b₁ образуют главную диагональ, а a₂, b₁- побочную диагональ.

Система двух линейных уравнений с двумя переменными

a₁x + b₁y = c₁                                при условии что, определитель системы ∆= a₁b₁   ≠ 0

a₂x + b₂y = c₂                                                                                                                                                 a₂b₂

и имеет единственное решение, которое находится по формуле

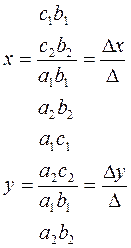    эти формулы называются «формулами Крамера»

Если ∆ =0, а ∆x ≠ ∆y ≠0, то система не имеет решений.

Если ∆ =∆x = ∆y =0, то система имеет бесконечное множество решений (R)

Билет №4

КВАДРАТНЫЕ УРАВНЕНИЯ И УРАВНЕНИЯ ПРИВОДИМЫЕ К НИМ.

Уравнения вида ax² + bx +c=0, где a, b, c-действительные числа, причем, а≠0, Х-переменная, называется квадратным уравнением.

Если, а=1, кв. уравнение называется приведённым.

Если, а≠0, то  неприведённым.

Квадратное уравнение вида ax²=0, ax²+c=0, ax²+bx=0 называется неполным.

Формула корней кв. уравнения ax² + bx +c=0 имеет вид

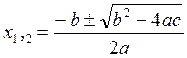, где b²-4ac=Д – дескрименант.

Билет №6

РЕШЕНИЕ КВАДРАТНЫХ НЕРАВЕНСТВ ГРАФИЧЕСКИ.

Графиком функции - парабола с ветвями вверх, при >0 и вниз, при <0. В зависимости от знака дескрименанта  уравнения ax² + bx +c=0 возможны три случая:

1)  Д>0, а>0, а<0 уравнение имеет два различных корня, и парабола пересекает ось ОХ в 2-х точках.

Д>0

а>0

                                      х

                      Д>0

                      а<0

2)  Д=0, а>0, а<0 уравнение имеет единственное решение, парабола касается оси ОХ

Д>0

а>0

 

                          Д=0        х

                          а<0

3)  Д<0, а>0, а<0. уравнение не имеет корней, парабола не пересекается  с осью ОХ

 

              Д<0

                а>0

                                                        х

                                  Д<0

                                  а<0

Билет №7

ОПРЕДЕЛИТЕЛЬ 3 ПОРЯДКА. СИСЕМА ТРЁХ ЛЕНЕЙНЫХ УРАВНЕНИЙ.

Определителем  3-гопорядка составленным из чисел a₁, b₁, c_1, а_2, b₂, c_2, a₃, b₃, c₃, называется число определяемое равенством:

          a₁b₁c₁

   ∆=  a₂b₂c₂  = a₁∙ b₂c₂   -b₁ a₂c₂   +c₁ c₂b₂

          a₃b₃c₃               b₃c₃            a₃c₃         a₃b₃

Последние выражение называется разложением определителя 3-го порядка по элементам первой строки.

Система 3-х линейных уравнений с 3-я переменными:                                                a₁b₁c₁

   A₁x+b₁y+ c₁z =d₁    При условии, что определитель системы не равен нулю ∆=    a₂b₂c₂    ≠ 0 и имеет

   A₂x+b₂y+c₂z =d₂       единственное решение которое находится по формуле:           a₃b₃c₃

   A₃x+b₃y+c₃z =d₃

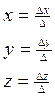_, где ∆х= d₂b₂c₂       ∆y=   a₂d₂c₂               ∆z = a₂d₂b₂

если ∆=0, а ∆х≠∆y≠∆z≠0, то Ø

если ∆=∆х=∆y=∆z=0, то R(множество решений)

Билет №8

РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.

Иррациональное уравнение – уравнение, содержащее переменную под знаком корня.

Решение иррационального уравнения основано на его преобразовании к рациональному уравнению, что достигается возведением обоих частей в одну и туже степень (иногда несколько раз). При возведении обоих частей уравнения в чётную степень получается уравнение  являющееся  следствием исходного.

Уравнению следствию удовлетворяют все корни исходного уравнения, но могут появиться и корни которые не являются корнями исходного уравнения («построили» корни).для выявления таких корней необходимо выполнить проверку. При возведении обеих частей уравнения в не чётную степень