Расчет оптимального плана перевозок продукции с трех складов нескольким потребителям

ТРАНСПОРТНАЯ  ЗАДАЧА

Вариант № 3

Имеется три склада,  содержащие однотипную продукцию. Имеется пять потребителей, которые нуждаются в этой продукции. Требуется найти такой план перевозок при котором общие затраты на перевозку всей продукции по всем потребителям будут минимальными.

а_i  -поставщики   в_j- потребители

Решение:

I

1.  Убедимся, что задача с правильным балансом:

3                        5

∑ _аi = 1600 > ∑ _вj    = 1420– Задача открытая. Необходимо ввести фиктивного

_{i= 1                           j = 1}                         потребителя : 1600-1420= 180

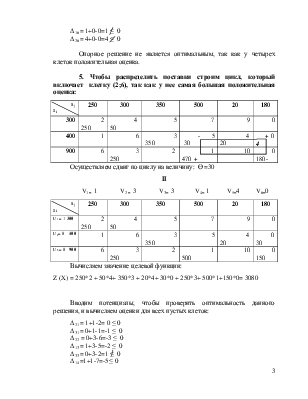
2.  Методом  минимальной стоимости построим опорное решение:

        2    4    5   7  9   0          
           С=  1    6    3   5  4   0    - Матрица стоимости

        6    3    2   1 10  0

В верхнем правом углу записываем стоимости единицы груза, а нижнем левом поставку. Число заполненных клеток должно быть: 3+6 -1= 8

 Вычисляем значение целевой функции:

Z (X) = 250*2+ 50* 4+ 350*3 + 30*5+ 20*4 + 250*3+ 470* 1+180*0= 3200

3. Вводим потенциалы, для того чтобы проверить оптимальность данного решения:

u _i = c _ij -v_j ; v_j= c _ij-u _i ; c _ij = u _i + v_j

      V₁₌   1                     V_{2 =}  3                      V₃₌  -1                  V₄₌ 1                     V₅₌0        V₆₌0

4.Вычисляем оценки для всех свободных клеток по формуле:

∆ _{ij =} u _i + v_j   -  c _ij          ∆ _ij  ≤  0

∆ ₂₁=  4+1-1= 4 ≤ 0

∆₃₁=  0+1-6=-6 ≤  0

∆ ₂₂ = 4+3-6= 1 ≤  0

∆ ₁₃= 1-1-5=-5   ≤  0

∆ ₃₃= 0-1-2=-3≤  0

∆ ₁₄=1+1-7=-5  ≤  0

∆ ₃₅= 0+0-10=-10 ≤  0

∆ ₁₆= 1+0-0=1 ≤  0

∆ ₂₆= 4+0-0=4 ≤  0

Опорное решение не является оптимальным, так как у четырех клеток положительная оценка.

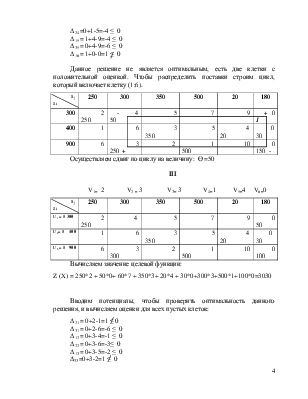
5. Чтобы распределить поставки строим цикл, который включает  клетку (2;6), так как у нее самая большая положительная оценка:

Осуществляем сдвиг по циклу на величину:  Ө =30

II

       V₁₌   1                     V_{2 =}  3                      V₃₌  3                    V₄₌ 1                V₅₌4          V₆₌0

Вычисляем значение целевой функции:

Z (X) = 250*2 + 50*4+ 350*3 + 20*4+ 30*0 + 250*3+ 500*1+150*0= 3080

Вводим потенциалы, чтобы проверить оптимальность данного решения, и вычисляем оценки для всех пустых клеток:

∆ ₂₁=  1+1-2= 0 ≤ 0

∆ ₃₁= 0+1-1=-1 ≤  0

∆ ₂₂ = 0+3-6=-3 ≤  0

∆ ₁₃= 1+3-5=-2 ≤  0

∆ ₃₃= 0+3-2=1 ≤  0

∆ ₁₄=1+1-7=-5≤  0

∆ ₂₄=0+1-5=-4 ≤  0

∆ ₁₅= 1+4-9=-4 ≤  0

∆ ₃₅= 0+4-9=-6 ≤  0

∆ ₁₆= 1+0-0=1 ≤  0

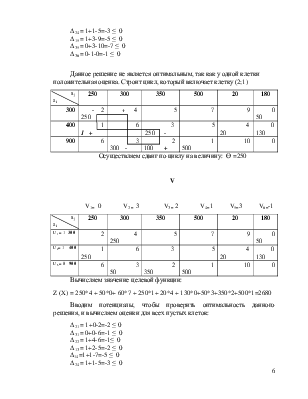
Данное решение не является оптимальным, есть две клетки с положительной оценкой. Чтобы распределить поставки строим цикл, который включает клетку (1;6).