Построение эпюр внутренних усилий в статически определимых балках и рамах. Расчет прочности изгибаемых железобетонных элементов по нормальным сечениям, страница 4

При Z₁=2.5  Mx ₁=35*2.5²/2-25=84.375 kHm

2)  Сечение AB; 2.6£Z₂³5.0

Mx₂=q*z₂²/2-m-p(z₂-2.5) (парабола)

При Z₂=2.5  Mx ₂=35*2.5²/2-25-25(2.5-2.5)=84.37 kHm

При Z₂=5.0  Mx ₂=35*5²/2-25-25(5-2.5)=350 kHm

5.  Вычисляем экстремальное значение изгибающего момента в сечениях FD иBC.

1) Определяем значение z в точке экстремума на отрезке BC

Qy₁=0; -q*z₁ =0

z=0

Определяем значение Mx в точке экстремума

Mx=q*z₁²/2-m =-25 kHm

2) Определяем значение z в точке экстремума на отрезке AB

Qy₂=0; p-q*z₂ =0

z=p/q

z=25/35=0.71

Определяем значение Mx в точке экстремума

Mx=q*z²/2-m-p(z-2.5)=35*0.71²/2-25-25(0.71-2.5)=28.57 kHm

6.  Подбираем сечение стальной балки прокатного профиля, проверяем сечения по нормальным, касательным и главным напряжениям. Строим эпюры.

Mmax=350kHm

Wx³Mmax/st=350*10³/240*10⁶=1458,3*10^-6 м³1458,3см³

Условию Wx³1458,3см³ удовлетворяет  Ι50 для которого::

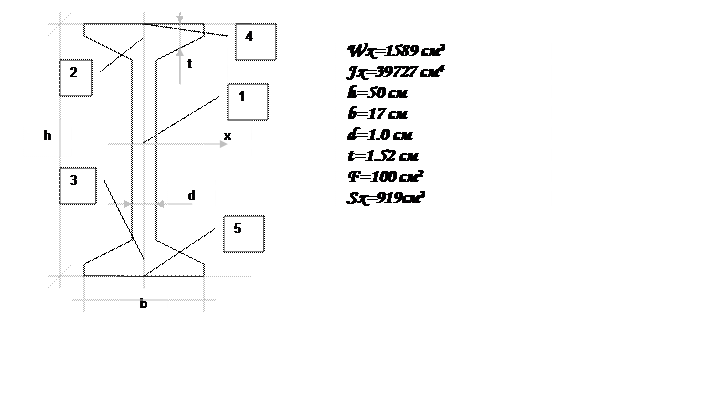
Построение эпюр  s и τ для сечения С  на участке  BC балки, где Q=150 kH;M=350 kHm, определяем напряжение в точках 1,2,3,4,5 сечения.

1.  Точка 1

y=0 ; Sx(о)=Sx ; s(o)=d

τ=Q*Sx/Jx*d=150*10³*919*10^-6/39727*10^-8*0.52*10^-2=34.7*10⁶=34.7 MПа

Главные напряжения:

s_1,3=s/2±1/2√s²+4τ²=±τ=±34,7 МПа

s₁=30,2 МПа ; s₃=-34,7 МПа

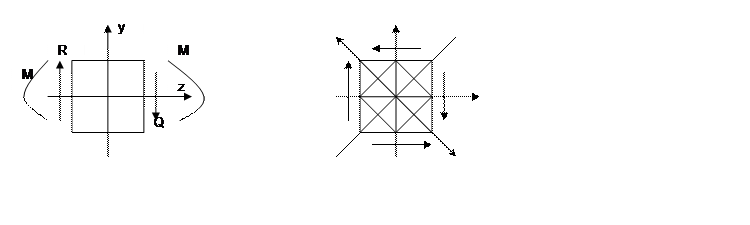
Направления главных площадок:

tg2α=-2τ/s=-2τ/0=-∞→ α=-45⁰

Расчетные напряжения

sэкв=s¹-s³=2τ=2*34,7=69,4 МПа

sэкв<st

Условие прочности выполняется.

2.  Точка 2 (стенка)

y=h/2 s(y)=d  Sx(y)=b*t/2(h-t)

s=-M(h/2-t)/Jx=350*10³(50/2-1.52)*10^-2/39727*10^-8=206860000 Па=-206,86 МПа

τ=Q*b*t(h-t)/2Jx*d=150*10³*17*1.52*(50-1.52)*10^-4/2*39727*10^-8*1*10-²=15.77 MПа

Главные напряжения

smax,min=-206,86/2±1/2√206,86²+4*15,77²=103,43±104,62

s₁=103,43+104,62=208,05 МПа

s₃=103,43-104,62=-1,19 МПа

Направление главных площадок:

tg2α=-2*15,77/206,86=0,152

α=1/2 arctg (0.152)=7⁰

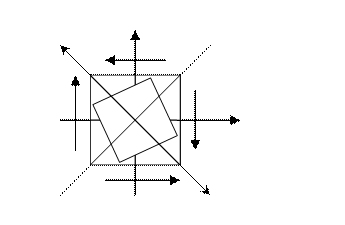
Расчетные напряжения

sэкв=s₁-s₃=208,05+1,19=209,24 МПа

sэкв<st

Условие прочности выполняется.

3.  Точка 2 (полка)

y-h/2-t  ; δ(y)=b ; Sx(y)=b*t/2(h-t)

s=-M(h/2-t)/Jx=-350*10³*(50/2-1.52)*10^-2/39727*10^-8=-206.86 МПа

τ=Q*t(h-t)/2Jx=150*10³*1.52(50-1.52)*10^-4/2*39727*10^-8=1.3 МПа

Главные напряжения

smax,min=-206,86/2±1/2√206,86²+4*1,3²=-103,42±103,44

s₁=-103,42+103,44=0.02 МПа

s₃=-103,42-103,44=206.86 МПа

Расчетные напряжения

sэкв= s₁-s₃=206,86+0,02=206,88 МПа

sэкв<st

Условие прочности выполняется.

4.  Точка 3 (стенка)

y=-(h-t) ; δ(y)=d ; Sx(y) =b*t/2(h-t)

s=M*(h/2-t)/Jx=350*10³*(50/2-1.52)*10^-2/39727*10^-8=206.86 МПа

τ=Q*b*t(h-t)/2Jx*d=150*10³*17*1.52*(50-1.52)*10^-4/2*39727*10^-8*1*10-²=15.77 MПа

Главные напряжения:

smax,min=206,86/2±1/2√206,86²+4*15,77²=103,42±104,62

s₁=103,42+104,62=208,04 МПа

s₃=103,42-106,62=-3,2 МПа

Направление главных площадок:

tg2α=-2*15,77/206,86=-0,152

α=1/2 arctg (-0.152)=-7⁰

Расчетные напряжения

sэкв= s₁-s₃=208,04+3,2=211,24 МПа

sэкв<st

Условие прочности выполняется.

5.  Точка 3 (полка)

y=-(h/2-t) ; δ(y)=b ;Sx(y)=b*t/2(h-t)

s=M*(h/2-t)/Jx=350*10³*(50/2-1.52)*10^-2/39727*10^-8=206.86 МПа

τ= Q*t(h-t)/2Jx=150*10³*1.52(50-1.52)*10^-4/2*39727*10^-8=1.3 МПа

Главные напряжения:

smax,min=-206,86/2±1/2√206,86²+4*1,3²=-103,42±103,44

s₃=-103,42+103,44=0.02 МПа

s₁=-103,42-103,44=206.86 МПа

Расчетные напряжения

sэкв= s₁-s₃=206,86-0,02=206,84 МПа

sэкв<st

Условие прочности выполняется.

6.  Точка 4

y=h/2 ; Sx(y)=0

s=-M*h/2Jx=-350*10³*25*10^-2/39727*10^-8=-220.25 МПа

τ=0

Главные  напряжения:

smax,min=-s/2±s/2=-220,25/2±220,25/2=-110,125±110,125

s₃=-110,125+110,125=0 МПа

s₁=110,125+110,125=220,25 МПа

Расчетные напряжения

sэкв= s₁-s₃=220,25-0=220,25 МПа

sэкв<st

Условие прочности выполняется

7.  Точка 5

y=-h/2 ; Sx(y)=0

s=M*h/2/Jx=350*10³*25*10^-2/39727*10^-8=220.25 МПа

τ=0

Главные напряжения:

s₁=s=220,25 МПа

s₃=0

Расчетные напряжения

sэкв= s₁-s₃=220,25-0=220,25 МПа

sэкв<st

Условие прочности выполняется

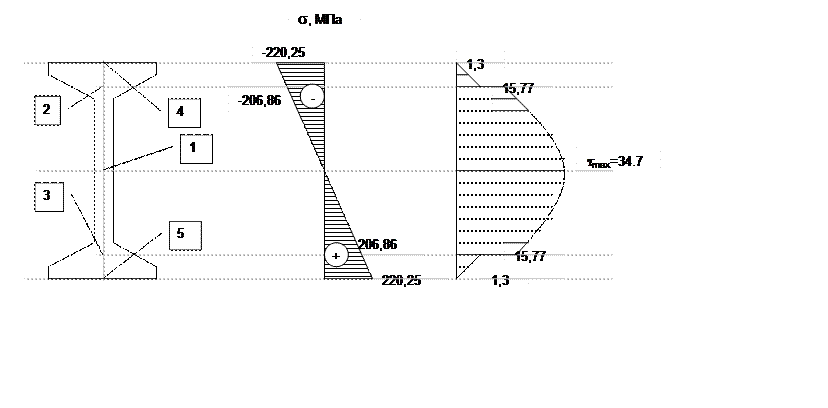
8.  Строим эпюры s и τ

τ , MПа