Построение эпюр внутренних усилий в статически определимых балках и рамах. Расчет прочности изгибаемых железобетонных элементов по нормальным сечениям, страница 2

При Z₂=2.0  Mx ₂=-25+35*2(2-1)-61.9*2=-78.8 kHm

При Z₂=3.8  Mx ₂=-25+35*2(3.8-1)-61.9*3.8=-64.22 kHm

3)  Сечение DB; 0£Z₃³2

Mx₃=-Rb*z₃ (прямая)

При Z₃=0  Mx ₃=-32.1*0=0 kHm

При Z₃=2  Mx ₃=-32.1*2=-64.2kHm

5.  Вычисляем экстремальное значение изгибающего момента в сечении AC.

Определяем значение z в точке экстремума

Qy₂=0 ;Ra-q*z=0

          61.9-35*z=0

z=61.9/35=1.8

Определяем значение  Mx  в точке экстремума

Mx= q*z₁²/2-Ra*z₁ = 35*1.8/2-61,9*1.8=54.72 kHm

1.0

 

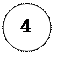
1.  Разделим раму на 2 характерных участка AB и BD

2.  Определим на каждом из участков в характерных сечениях N(нормальную силу), Q(поперечную силу), M(момент).

1)  Участок AB

Сечение A:

N=-22 kH

Q=0 kH

M=0 kHm

Сечение B:

N=-22 kH

Q=6*0.9=5.4 kH

M=6*0.9*0.45=2.43 kHm

2)  Участок BD

Сечение В:

N=-6*0.9=-5.4kH

Q=-22 kH

M =6*0.9*0.45=2.43 kHm

Сечение С:

N=-6*0.9=-5.4 kH

Q=-22 kH

M^в=6*0.9*0.45-22=-19.53 kHm

M^н=6*0.9*0.45-22+10=-9.53 kHm

Сечение D:

N=-6*0.9=-5.4 kH

Q=-22 kH

M=6*0.9*0.45+10-22*2=-31.57 kHm

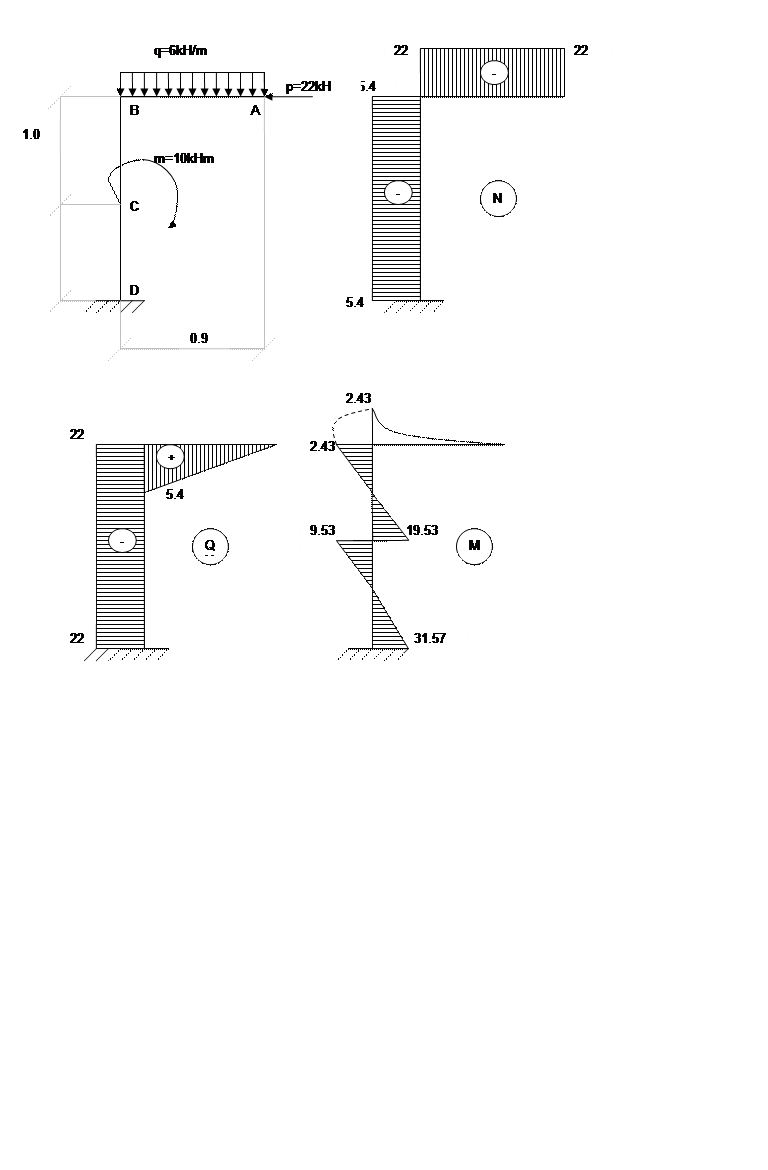
1.  Определяем опорные реакции.

SMa=0; p*1.2+m-Rb*6+q*1.2*(2.4+1.2*2.3)=0

Rb=(15*1.2+24+35*1.2*3.2)/6=29.4kH

SMb=0; m+Ra*6-p*4.8-q*1.2*(2.4+0.4)=0

Ra=(15*4.8-24+35*1.2*2.8)/6=27.6kHm

Выполним проверку

Sy=0

Ra+Rb-p-q*1.2=0

27.6+29.4=15+35*1.2

57=57

2.  Намечаем характерные сечения.

Разделим балку на пять характерных сечений: отрезки AC, CD, DE, EF и FB.

3.  Определяем поперечные силы в характерных сечениях и находим их значение на концах характерных отрезков.

1)  Сечение AC; 0£Z₁³1.2

Qy₁=Ra(const)

При Z₁=0  Qy₁=27.6 kH

При Z₁=1.2  Qy₁=27.6 kH

2)  Сечение CD; 1.2£Z₂³2.4

Qy₂=Ra-p (const)

При Z₂=1.2  Qy₂=27.6-15=12.6kH

При Z₂=2.4  Qy₂=27.6-15=12.6 kH

3)  Сечение DE; 2.4£Z₃³3.6

Qy₃= Ra-p-q*(z₃-2.4) (прямая)

При Z₃=2.4  Qy₃=27,6-15-35(2,4-2,4)=12.6 kH

При Z₃=3.6  Qy₃=27,6-15-35(3.6-2,4)=12.6 kH

4)  Сечение FB; 0£Z₄³1.2

Qy₄=-Rb(const)

При Z₄=0  Qy₄=-29.4 kH

При Z₄=1.2  Qy₄=-29.4 kH

5)  Сечение EF; 1.2£Z₅³2.4

Qy₅=-Rb(const)

При Z₅1.2  Qy₅=-29.4kH

При Z₅₌2,4  Qy₅=-29.4kH

4.  Определяем изгибающие моменты в характерных сечениях и находим их значение на концах характерных отрезков.

1)  Сечение AC; 0£Z₁³1.2

Mx₁=-Ra*z₁ (прямая)

При Z₁=0  Mx₁=-27.6*0=0 kHm

При Z₁=1.2  Mx₁=-27.6*1.2=-33.12kHm

2)  Сечение CD; 1.2£Z₂³2.4

Mx₂=p*(z₂-1.2)- Ra*z₂ (прямая)

При Z₂=1.2  Mx ₂=15(1.2-1.2)-27.6*1.2=-33.12 kHm

При Z₂=2.4  Mx ₂=15(2.4-1.2)-27.6*2.4=-48.24 kHm

3)  Сечение DE; 2.4£Z₃³3.6

Mx₃= p*(z₃-1.2) -Ra*z₃+q*(z₃-2.4)²/3 (парабола)

При Z₃=2.4  Mx ₃=15*(2,4-1,2)-27,6*2,4+35*(2,4-2,4)²/3=-48,24 kHm

При Z₃=3.6  Mx ₃=15*(3,6-1,2)-27,6*3,6+35*(3,6-2,4)²/3=-46,56  kHm

4)  Сечение FB; 0£Z₄³1.2

Mx₄=-Rb*z₄ (прямая)

При Z₄=0  Mx ₃=-29,4*0=0 kHm

При Z₄=1.2  Mx ₃=-29,4*1,2=-35,28 kHm

5)  Сечение EF; 1.2£Z₅³2.4

Mx₅=m-Rb*z₅ (прямая)

При Z₅=1.2  Mx₅=24-29.4*1.2=-11.28 kHm

При Z₅=2.4  Mx₅=24-29.4*2.4=-46.56 kHm

5.  Вычисляем экстремальные значения изгибающего момента в сечении DE.

1) Определяем значение z в точке экстремума на отрезке DE

Qy₃=0 ; Ra-p-q*(z₃-2.4)=0

          27,6-15-35(z-2,4)=0

z=(27.6-15)/35+2.4=2.76

Определяем значение  Mx  в точке экстремума

Mx₃=p*(z₃-1.2)-Ra*z₃+q*(z₃-2.4)²/3=15*(2.76-1,2)-27,6*2.76+35*(2.76-2,4)²/3=-51.27 kHm

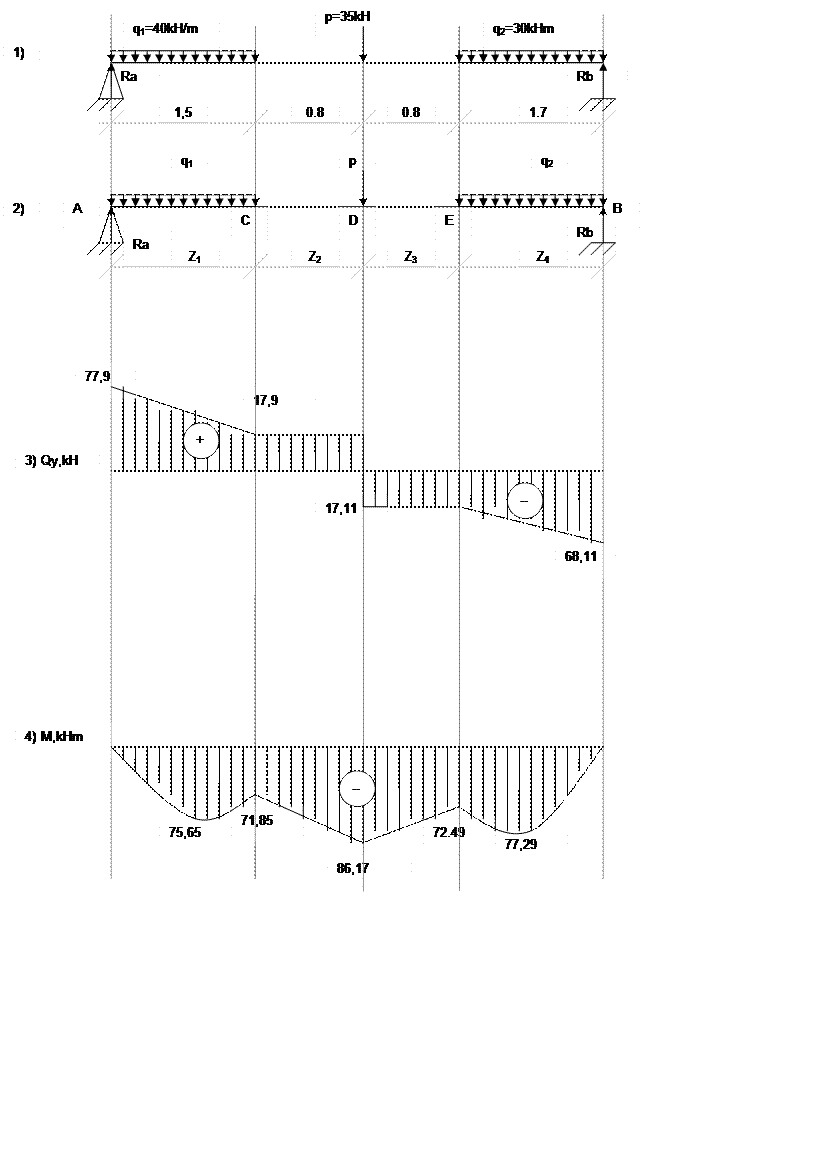
6.  Определяем опорные реакции.

SMa=0; -q₁*1.5*0.75-p(0.8+1.5)-q₂*1.7*3.95+Rb*4.8=0

Rb=(40*1.5*075+35*2.3+30*1.7*3.95)/4.8=68.1 kH

SMb=0; -Ra*4.8+q₁*1.5*4.05+q₂*1.7*0.85+p*2.5=0

Ra=(40*1.5*4.05+30*1.7*0.85+35*2.5)=77.9 kHm

Выполним проверку

Sy=0

Ra+Rb-p-q₁*1.5-q₂*1.7=0

68.1+77.9=35+40*1.5+30*1.7

146=146

7.  Намечаем характерные сечения.

Разделим балку на четыре характерных сечения: отрезки AC, CD, DE и EB.

8.  Определяем поперечные силы в характерных сечениях и находим их значение на концах характерных отрезков.

1)  Сечение AC; 0£Z₁³1.5

Qy₁=Ra-q₁*z₁(прямая)