МИНИСТЕРСТВО ОБРАЗОВАНИЕ РОССИЙСКОЙ ФЕДЕРАЦИИ
Московский Государственный Строительный Университет
Кафедра Железобетонных конструкций
КУРСОВОЙ ПРОЕКТ
«Основы конструирования и проектирования»
Проверил:
Тамразян А.Г.
Выполнила:
студентка ЭОУС 4-1 в/о
Бойкова Т.С.
Москва 2005
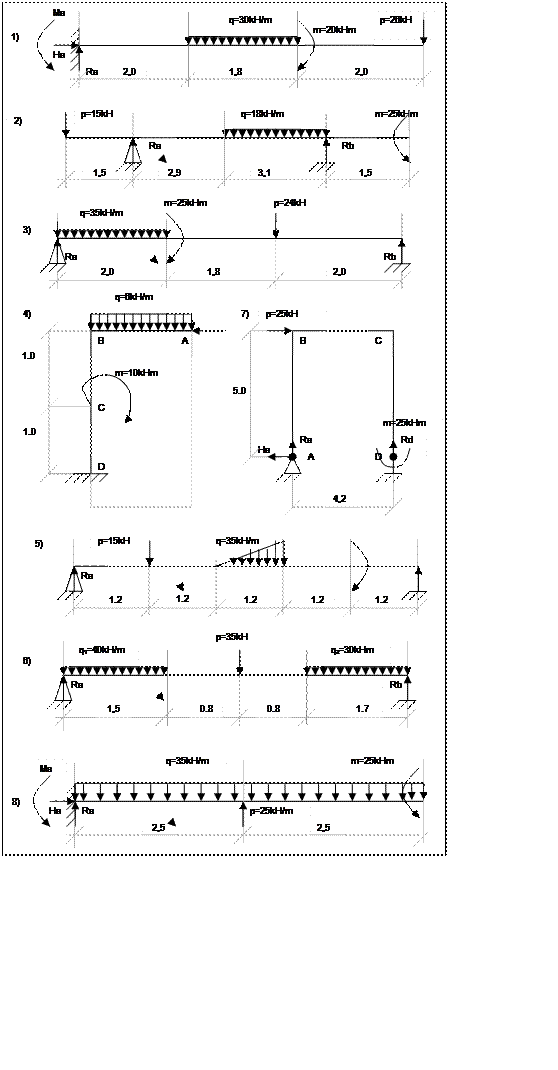
Целью курсового проекта является построение эпюр внутренних усилий, то есть :N (нормалей), Q (поперечных сил) и M (изгибающих моментов) в статически определимых балках и рамах и последующий расчет прочности изгибаемых железобетонных элементов по нормальным сечениям.для заданных балок и рам.
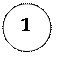
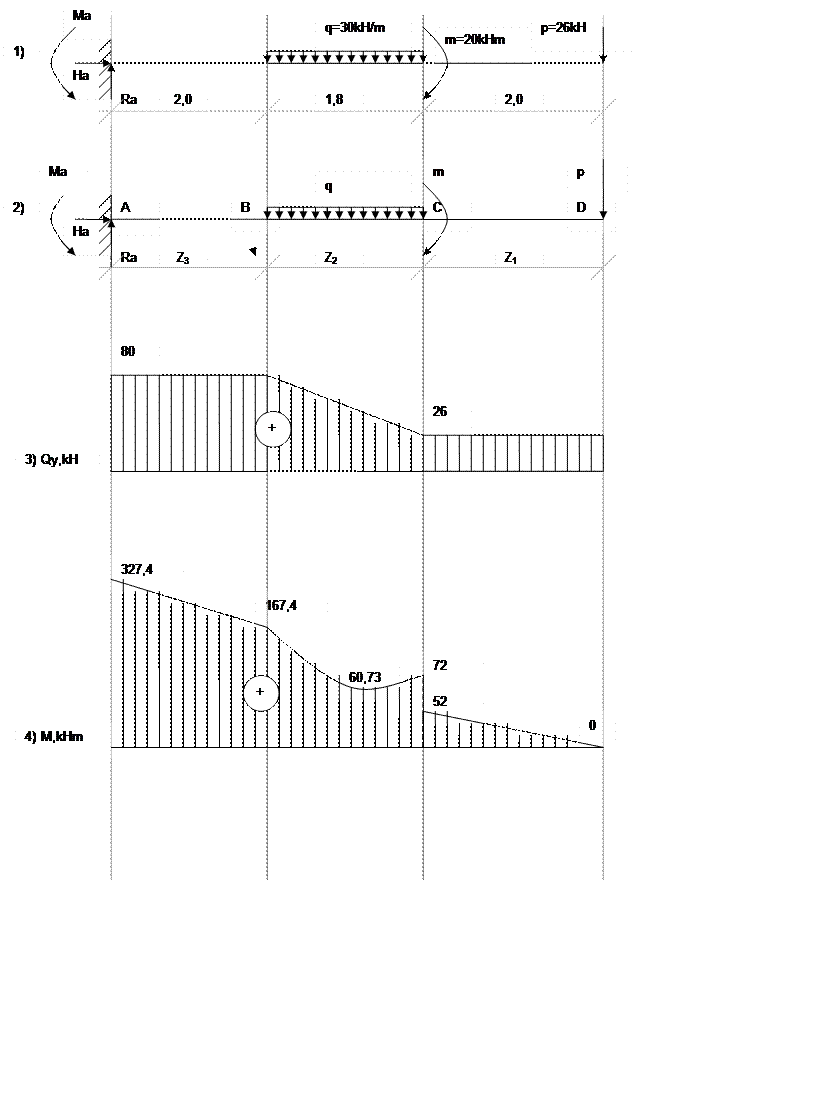
1. Определяем опорные реакции.
Ha=0
Sy=0; Ra-p-q*1.8=0
Ra=p+q*1.8=26+30*1.8=80 kH
SM=0; Ma-p*5.8-m-q*1.8*2.9=0
Ma=p*5.8+m+q*1.8*2.9=26*5.8+20+30*1.8*2.9=327.4 kHm
2. Намечаем характерные сечения.
Разделим балку на три характерных сечения: отрезки АВ, ВС и СД.
3. Определяем поперечные силы в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение CD; 0£Z1³2.0
Qy1=p (const)
При Z1=0 Qy1=26 kH
При Z1=2,0 Qy1=26 kH
2) Сечение BC; 2.0£Z2³3.8
Qy2=p+q(z2-2) (прямая)
При Z2=2.0 Qy2=26+30*(2-2)=26 kH
При Z2=3.8 Qy2=26+30(3,8-2)=80 kH
3) Сечение AB; 3.8£Z3³5.8
Qy3=p+q*1.8 (const)
При Z3=3.8Qy3=26+30*1.8=80 kH
При Z3=5.8Qy3=26+30*1.8=80 kH
4. Определяем изгибающие моменты в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение CD; 0£Z1³2.0
Mx1=p*z1 (прямая)
При Z1=0 Mx1=26*0=0 kHm
При Z1=2,0 Mx 1=26*2=52 kHm
2) Сечение BC; 2.0£Z2³3.8
Mx2=p*z2+m+q(z2-2)2/2 (парабола)
При Z2=2.0 Mx 2=26*2+20+30*(2-2)2/2=72 kHm
При Z2=3.8 Mx 2=26*3,8+20+30*(3,8-2)2/2=167,4 kHm
3) Сечение AB; 3.8£Z3³5.8
Mx3=p*z3+q*1.8(z3-2.9)+m (прямая)
При Z3=3.8 Mx 3=26*3,8+30*1.8(3,8-2,9)+20=167,4 kHm
При Z3=5.8 Mx 3=26*5,8+30*1.8(5,8-2,9)+20=327,4 kHm
5. Вычисляем экстремальное значение изгибающего момента в сечении BC.
Определяем значение z в точке экстремума
Qy2=0 ;p+q(z2-2)=0
26+30(z-2)=0
26+30z-30*2=0
z=(30*2-26)30=1.13
Определяем значение Mx в точке экстремума
Mx=p*z+m+q(z-2)2/2= 26*1.13+20+30*(1.13-2)2/2=60.73 kHm
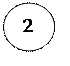
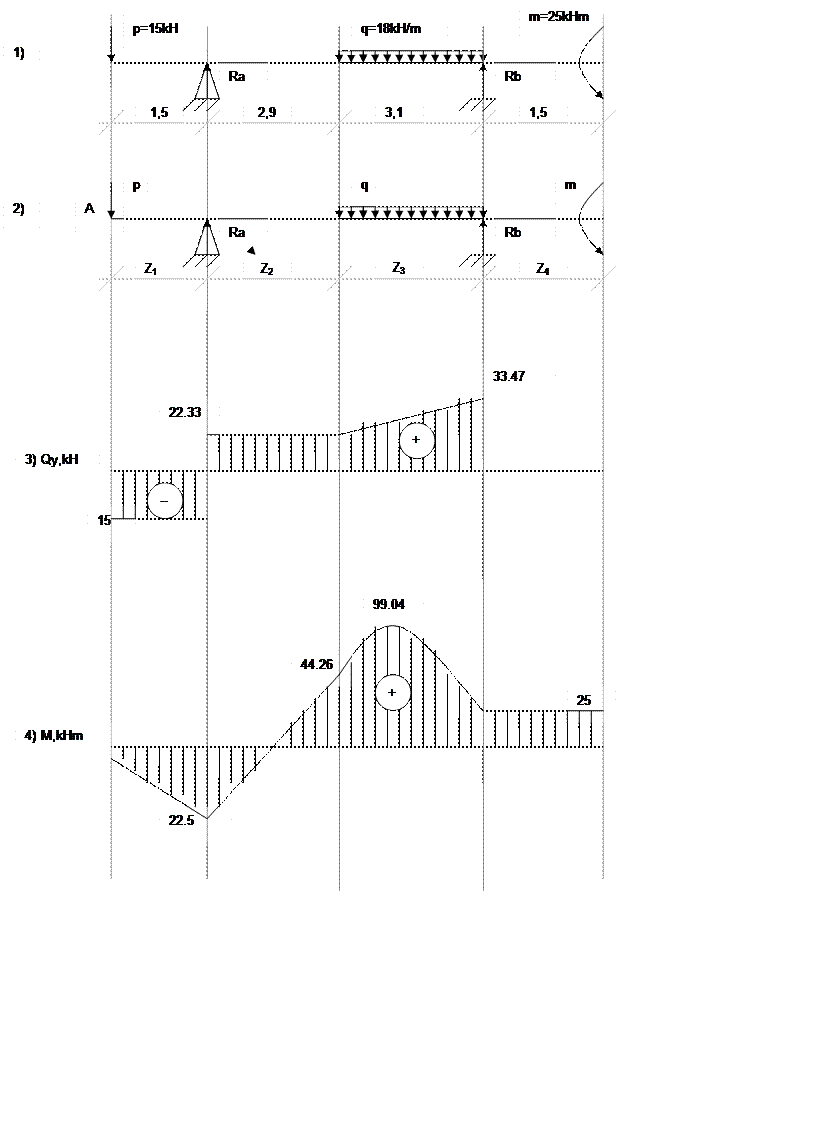
1. Определяем опорные реакции.
SMa=0; p*1.5-q*3.1(2.9+1.55)+m+Rb*6=0
Rb=(-15*1.55+18*3.1*4.45-25)/6=33.47 kH
SMb=0; p*7.5-Ra*6+q*3.1*1.55+m=0
Ra=(15*7.5+18*3.1+25)/6=37.33 kHm
Выполнимпроверку
Sy=0
Ra+Rb-q*3.1-p=0
37.33+33.47=18*3.1+15
70.8=70.8
2. Намечаем характерные сечения.
Разделим балку на четыре характерных сечения: отрезки KA, АC, СB и BD.
3. Определяем поперечные силы в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение KA; 0£Z1³1.5
Qy1=-P (const)
При Z1=0 Qy1=-15 kH
При Z1=1.5 Qy1=-15 kH
2) Сечение AC; 1.5£Z2³4.4
Qy2=-p+Ra (const)
При Z2=1.5 Qy2=37.33-15=22.33 kH
При Z2=4.4 Qy2=37.33-15=22.33 kH
3) Сечение CB; 4.4£Z3³7.5
Qy3=Ra-p-q(z2-4.4) (прямая)
При Z3=4.4 Qy3=37.33-15*18*(4.4-4.4)=22.33 kH
При Z3=7.5 Qy3=37.33-15*18*(7.5-4.4)=33.47 kH
4) Сечение BD; 0£Z4³1.5
Qy4=0 (const)
При Z4=0 Qy3=0 kH
При Z4=1.5 Qy3=0 kH
4. Определяем изгибающие моменты в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение KA; 0£Z1³1.5
Mx1=-p*z1(прямая)
При Z1=0 Mx1=-15*0=0 kHm
При Z1=1.5 Mx1=-15*1.5=-22.5 kHm
2) Сечение AC; 1.5£Z2³4.4
Mx2= Ra*(z2-1.5) -p*z2 (прямая)
При Z2=1.5 Mx 2=37.33(1.5-1.5)-15*1.5=-22.5 kHm
При Z2=4.4 Mx 2=37.33(4.4-1.5)-15*4.4=42.26 kHm
3) Сечение CB; 4.4£Z3³7.5
Mx3=Ra*(z3-0.5)-p*z3-q(z3-4.4)2/2 (парабола)
При Z3=4,4 Mx 3=37.33(4.4-1.5)-15*4.4-18(4.4-4.4)2/2=42.26 kHm
При Z3=7,5 Mx 3=37.33(7.5-1.5)-15*7.5-18(7.5-4.4)2/2=24.99 kHm
4) Сечение DB; 0£Z4³1.5
Mx4=m (const)
При Z4=0 Mx 3=25kHm
При Z4=1.5Mx 3=25kHm
5. Вычисляем экстремальное значение изгибающего момента в сечении CB.
Определяем значение z в точке экстремума
Qy2=0 ; Ra-p-q*(z-4.4)=0
37.33-15-18*(z-4.4)=0
z=(37.33-15)/18+4.4=1.2
Определяем значение Mx в точке экстремума
Mx=Ra*(z3-0.5)-p*z3-q(z3-4.4)2/2 =37.33(1.2-1.5)-15*1.2-18(1.2-4.4)2/2=99.04 kHm
6. Рассчитаем прочность изгибаемых железобетонных элементов по нормальным сечениям
1. Mx =99,04 kHm
b*h=25*50cm
Арматура класса А-III, бетон тяжелый Б20
Rb=11.5 MПа ; Rs=Rsсж=355 МПа
Mb=0.85
a=4 cm
h0=h-a=50-4=46 cm
αm=M/Rs*b*h02=9904000/0.85*11.5*462*25*100=0.192
2. По таблице расчета изгибаемых элементов прямоугольного сечения подбираем соответствующий коэффициент.
ξ=0,89
η=1-ξ/2=1-0,89/2=0,555
As=M/Rs*η*h0=9904000/355*0.555*46*100=10.93 cm2
3. По таблице расчетных площадей поперечных сечений и массы арматуры подбираем количество и диаметр необходимой арматуры для нашей нагрузки.
Количество арматуры :10шт ,d=12mm As=11.31cm2
10 12
х=ξ* h0=0,89*46=40,94
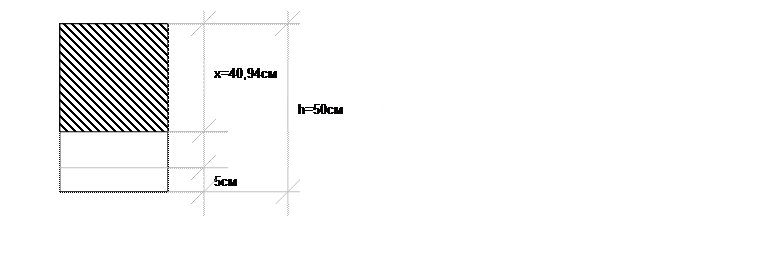

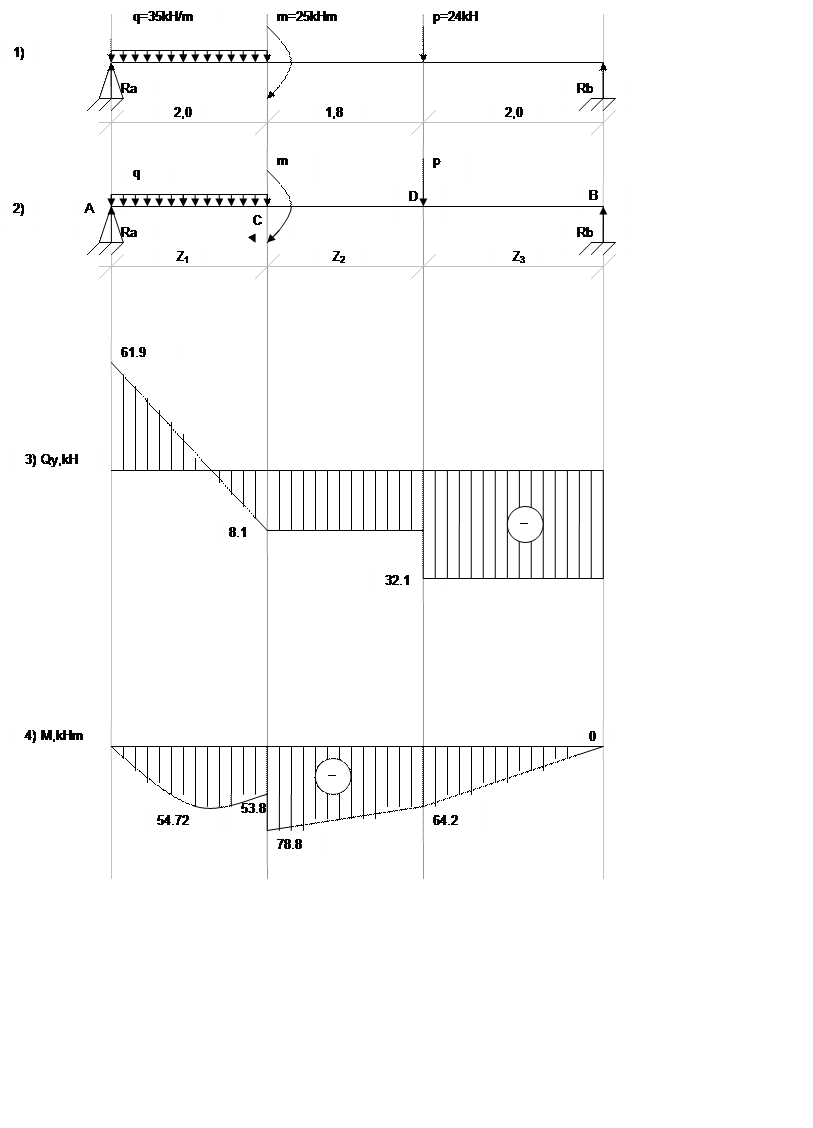
1. Определяем опорные реакции.
SMa=0; q*2*1+p*3.8+m-Rb*5.8=0
Rb=(70+24*3.8+25)/5.8=32.1kH
SMb=0; Ra*5.8-q*2*4.8+m-p*2=0
Ra=(35*2*4.8+24*2-25)/5.8=61.9kHm
Выполним проверку
Sy=0
Ra+Rb-q*2-p=0
32.1+61.9=35*2+24
94=94
2. Намечаем характерные сечения.
Разделим балку на три характерных сечения: отрезки АC, СD и DB.
3. Определяем поперечные силы в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение AC; 0£Z1³2.0
Qy1=Ra-q*z (прямая)
При Z1=0 Qy1=61,9-35*0=61,9 kH
При Z1=2,0 Qy1=61,9-35*2=-8,1 kH
2) Сечение CD; 2.0£Z2³3.8
Qy2=Ra-q2 (const)
При Z2=2.0 Qy2=61.9-35*2=-8.1 kH
При Z2=3.8 Qy2=61.9-35*2=-8.1 kH
3) Сечение DB; 0£Z3³2
Qy3=-Rb (const)
При Z3=0 Qy3=-32.1 kH
При Z3=0 Qy3=-32.1 kH
4. Определяем изгибающие моменты в характерных сечениях и находим их значение на концах характерных отрезков.
1) Сечение AC; 0£Z1³2.0
Mx1=q*z12/2-Ra*z1 (парабола)
При Z1=0 Mx1=35*0/2-61,9*0=0 kHm
При Z1=2 Mx1=35*2/2-61,9*2=-53,8 kHm
2) Сечение CD; 2.0£Z2³3.8
Mx2=-m+q*2(z2-1)-Ra*z2 (прямая)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.