Инвестиции в облигации: оценка и доходность облигаций

Вопрос 71. Инвестиции в облигации: оценка и доходность облигаций.

Оценка облигаций. Облигация может приносить доход двумя способами: - в форме процентной ставки (купона) по займу; -м/достичь прироста капитала, который представляет собой разницу между ценой, по которой инвестор продает облигацию, и ценой, по которой облигация была приобретена.

Облигации с момента их эмиссии и до погашения продаются и покупаются по установившимся на рынке ценам.

Рыночная цена – цена, по которой облигации продаются и покупаются на денежно-кредитном рынке с момента их эмиссии  до погашения. Поскольку номиналы у разных облигаций существенно различаются между собой, показателем сопоставимости является курс олб-ции - цена облигации в расчете на 100 ден единиц номинала:

где K – курс облигации; Р – рыночная цена; N – номинал облигаций.

Определение курсовой стоимости облигаций Р основано на принципе дисконтирования доходов, так как именно дисконтированная (приведенная) стоимость всех доходов, которую предполагает получить инвестор с момента покупки облигации и до ее погашения, определяет рыночную цену облигации на момент ее приобретения.

Бескупонные облигации. Будущая выплата – это номинал облигации N. Разность между номиналом и текущей ценой продажи называется облигационной скидкой (дисконтом). Так как облигация с нулевым купоном создает только один будущий денежный поток доходов, который равен ее номинальной стоимости, то ее цена Р есть приведенная стоимость номинальной стоимости облигации. Если номинальная стоимость должна быть получена через n лет от настоящей даты, то при годовой процентной ставке для дисконтирования r цена чисто дисконтной облигации равна

 где  – дисконтированная стоимость одной будущей денежной единицы.

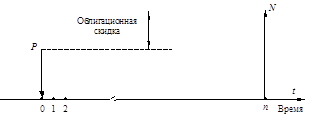
Рис. 1. Денежные потоки для чисто дисконтной облигации

Купонные облигации - облигации, по кот один или два раза в год производятся купонные выплаты, а в момент погашения выплачивается номинал. Допустим, что сегодня приобретается облигация с номинальной стоимостью N и сроком погашения через n лет. Предположим, что в конце каждого года до срока погашения по облигации выплачивается купонный доход С; соответствующая ставка дохода – r. Тогда приведенная стоимость потока купонных платежей равна

 где  – дисконтированная стоимость ежегодной ренты (аннуитета) в 1 ден. ед.

Приведенная стоимость возвращаемых в момент погашения облигации платежей по номиналу составит .

Принимая во внимание, что цена купонной облигации должна быть равна сумме величин приведенной стоимости выплат, которые надлежит произвести по облигации, цену купонной облигации можно рассчитать следующим образом:

Отметим при этом еще раз, что купонные выплаты по облигации представляют собой обычный аннуитет, приведенную стоимость которого можно рассчитать по формуле (n – количество лет):

.  

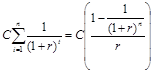
                                                  Рис. 2. Денежные потоки для купонной облигации

В том случае, если купон выплачивается несколько раз в год (m > 1), формула для расчета стоимости облигации будет иметь вид:

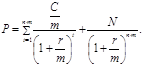
Соотношение между величинами купонной ставки, требуемой доходности и ценой м/конкретизировать с помощью следующих правил.

П1: Если требуемая доходность равна купонной ставке по облигации, то ее цена равна номиналу. П2: Если требуемая доходность выше, чем купонная ставка по облигации, то цена облигации меньше номинала, т. е. облигация продается с дисконтом к номиналу. П3: Если требуемая доходность меньше, чем купонная ставка, то ее цена больше номинала, т. е. облигация продается с премией к номиналу. П4: Цены облигаций изменяются в направлении, противоположном направлению изменения доходностей.

Цена как функция срока до погашения. Цена облигации не будет оставаться неизменной, если облигация продается с дисконтом или с премией. Цена любого выпуска облигаций к моменту погашения их достигает номинала N, рис.3.

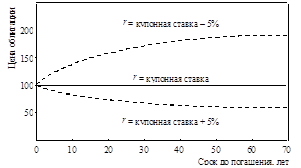Рис. 3. Цена как функция срока до погашения.