Инвестиции в облигации: оценка и доходность облигаций, страница 2

Цена облигации, продающейся с дисконтом, при условии неизменной требуемой доходности растет. Обратный процесс происходит с ценой облигации, продающейся с премией. Цена обеих облигаций в момент погашения равняется номинальной стоимости. Симметричные разности между требуемой доходностью и купонной ставкой преобразуются в асимметричные разности между ценой облигации и ее номинальной стоимостью. В частности, цена облигации при снижении доходности растет в бóльшей степени, чем она падает при росте доходности.

Доходность облигаций. В общем случае под доходностью любой инвестиции понимается процентная ставка, которая позволяет уравнять приведенную стоимость денежных потоков конкурентной инвестиции с ценой (стоимостью) инвестиции.

Доходность бескупонной облигации – это годовая ставка процента, получаемая инвестором, купившим и владеющим данной облигацией до момента ее погашения.

Если  то .

Определение доходности по купонной облигации. Для купонной облигации различают текущую доходность и внутреннюю ставку дохода или доходность к погашению.

Текущая доходность определяется по формуле:

где              rт – текущая доходность;

С – купонный доход по облигации (купон);

Р – текущая цена облигации.

Внутреннюю доходность можно рассчитывать по формуле оценки рыночной цены облигации:

К сожалению, данное уравнение не решается в конечном виде: определить доходность можно только с помощью специальной компьютерной программы.

М/воспользоваться методом подстановки в формулу цены облигации различных значений внутренней доходности с расчетом соответствующих им цен. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадет с заданной ценой облигации. Блок-схема алгоритма данного расчета приводится на рис. 4.

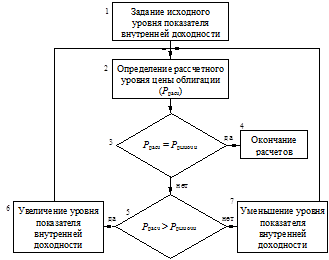
Рис. 4. Алгоритм расчета дох-ти купонной облигации

В ряде случаев для принятия финансового решения достаточно определить только приближенный (ориентировочный) уровень доходности облигации. Он может быть использован в качестве исходного уровня доходности в первом блоке рассмотренного выше алгоритма.

Традиционно используемая формула расчета приближенного уровня доходности облигации имеет вид:

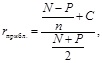
где              r – внутренняя доходность (доходность к погашению); N – номинальная стоимость облигации; Р – цена облигации; n – количество лет до погашения; С – купонный доход;

В ряде случаев лучшее приближение дает формула Р.  Род­ри­геса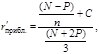

Эта формула дает хорошее приближение при условии невысокого уровня купонной ставки (ниже 50% годовых) и близких значений цены облигации и ее номинальной стоимости. В частности, если цена отличается от номинала более чем в 2 раза, то применение обеих формул расчета приближенных оценок недопустимо.

Погрешность расчетов по формулам приближенных оценок тем выше, чем больше лет остается до погашения облигации.

Для ускорения процесса расчета внутренней доходности облигации может быть использована также формула линейной интерполяции:

где              r₁, r₂ – значения соответственно заниженного и завышенного уровней ориентировочной доходности облигаций; Р₁, Р₂ – расчетные рыночные цены облигации, соответствующие уровням доходности r₁ и r₂;

Р – фактическая (действительная) цена облигации на фондовом рынке.

Резюмируя вышесказанное, отметим, что доходность к погашению позволяет оценить не только текущий (купонный) доход, но и размер прибыли или убытка, ожидающих капитал инвестора, остающегося владельцем облигации до ее погашения эмитентом. Кроме того, доходность к погашению принимает в расчет временные параметры денежных потоков.

Соотношение основных параметров облигации