Физика \ Физико-химические основы технологии электронных средств

Определение физико-химических параметров полупроводников, страница 2

·  для плоскостей (110) и (100):

ns(h,k,l) = χ в(s) · +  χ р(s) · + χ г(s)·1,                                                                                                            (19)

где h, k , l  –  индексы Миллера;

·  для плоскости (111):

ns(h,k,l) = χ в(s) · +  χ р(s)  +  χ г(s)·1,                                                                                                            (19)

  χ в(s) , χ р(s) , χ г(s)  - число атомов (или молекул) вещества соответственно в

                                вершине, на ребре или грани поверхности, ограниченной

                                объемом элементарной ячейки и определяемой индексами

                                     Миллера:

  1.  Площадь поверхности элементарной ячейки в различиях направлениях, определяемой индексом Миллера h, k, l  для кубической системы:

·  в направлении [100] , Å2,

S(100) =  a2                                                                                                                                                                  (20)

·  в направлении  [110] , Å2,

S(110) = a2                                                                                                             (21)

·  в направлении  [111] , Å2,

S(111) =  a2                                                                                                   (22)

27.Поверхностная плотность атомов (или молекул) для различных кристаллографических направлений, определяемых индексами Миллера для кубической системы;

в направлении [100] , см -2,

NS(100) =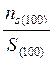                                                                                                             (23)

в направлении [110] , см -2,

NS(110) =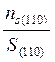                                                                                   (24)

в направлении [111] , см -2,

NS(111) =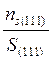                                                                                    (25)

28.Коэффициент упаковки (модель касающихся сфер, заполняющих элементарную ячейку, %)      

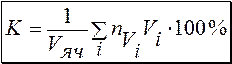                    , где                    (26)

                    Vяч- объём элементарной ячейки, Vi-объём структурной единицы (атома или молекулы, nVi – число атомов в ячейке, i- число видов атомов)

                           

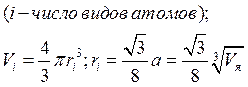
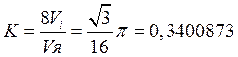
29.

Число свободных связей на поверхности элементарной ячейки

(100)

2

(110)

4

(111)

3

Плотность свободных связей на поверхности элементарной ячейки

(100)

(110)

 

(111)

 

30.Объем твердой сферы – параметр в уравнении состояния Ван-дер-Ваальса (объем Бойля) - в соответствии с моделью жестких параллельных кубов, см3/моль,

b = 4V0NA = 4VM(s)                                                                                                              (26)

31. Критический молярный объем вещества в соответствии с уравнением состояния Ван-дер-Ваальса, см3/моль,

VM(кр) = 3b = 12VM(s)                                                                                                         (27)

32. Критическая плотность вещества по определению, г/см3,

ρm(кр) =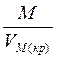                                                                                                             (28)

Скачать файл